Capacitors and calculus

Capacitors do not have a stable "resistance" as conductors do. However, there is a definite mathematical relationship between voltage and current for a capacitor, as follows:

The lower-case letter "i" symbolizes instantaneous current, which means the amount of current at a specific point in time. This stands in contrast to constant current or average current (capital letter "I") over an unspecified period of time. The expression "dv/dt" is one borrowed from calculus, meaning the instantaneous rate of voltage change over time, or the rate of change of voltage (volts per second increase or decrease) at a specific point in time, the same specific point in time that the instantaneous current is referenced at. For whatever reason, the letter v is usually used to represent instantaneous voltage rather than the letter e. However, it would not be incorrect to express the instantaneous voltage rate-of-change as "de/dt" instead.

In this equation we see something novel to our experience thusfar with electric circuits: the variable of time. When relating the quantities of voltage, current, and resistance to a resistor, it doesn't matter if we're dealing with measurements taken over an unspecified period of time (E=IR; V=IR), or at a specific moment in time (e=ir; v=ir). The same basic formula holds true, because time is irrelevant to voltage, current, and resistance in a component like a resistor.

In a capacitor, however, time is an essential variable, because current is related to how rapidly voltage changes over time. To fully understand this, a few illustrations may be necessary. Suppose we were to connect a capacitor to a variable-voltage source, constructed with a potentiometer and a battery:

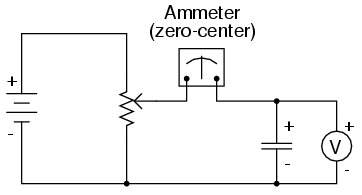
If the potentiometer mechanism remains in a single position (wiper is stationary), the voltmeter connected across the capacitor will register a constant (unchanging) voltage, and the ammeter will register 0 amps. In this scenario, the instantaneous rate of voltage change (dv/dt) is equal to zero, because the voltage is unchanging. The equation tells us that with 0 volts per second change for a dv/dt, there must be zero instantaneous current (i). From a physical perspective, with no change in voltage, there is no need for any electron motion to add or subtract charge from the capacitor's plates, and thus there will be no current.

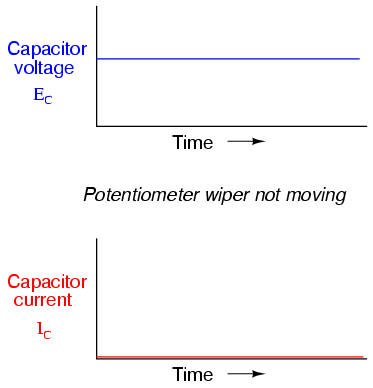
Now, if the potentiometer wiper is moved slowly and steadily in the "up" direction, a greater voltage will gradually be imposed across the capacitor. Thus, the voltmeter indication will be increasing at a slow rate:

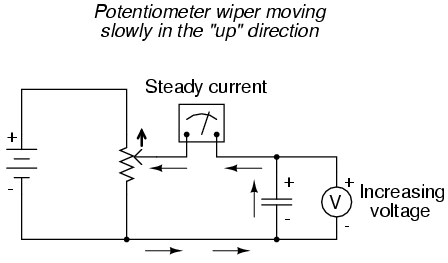
If we assume that the potentiometer wiper is being moved such that the rate of voltage increase across the capacitor is steady (for example, voltage increasing at a constant rate of 2 volts per second), the dv/dt term of the formula will be a fixed value. According to the equation, this fixed value of dv/dt, multiplied by the capacitor's capacitance in Farads (also fixed), results in a fixed current of some magnitude. From a physical perspective, an increasing voltage across the capacitor demands that there be an increasing charge differential between the plates. Thus, for a slow, steady voltage increase rate, there must be a slow, steady rate of charge building in the capacitor, which equates to a slow, steady flow rate of electrons, or current. In this scenario, the capacitor is acting as a load, with electrons entering the negative plate and exiting the positive, accumulating energy in the electric field.

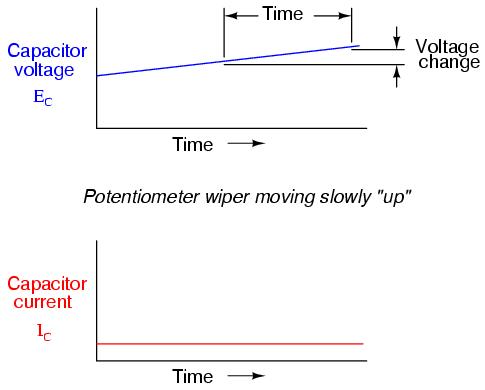
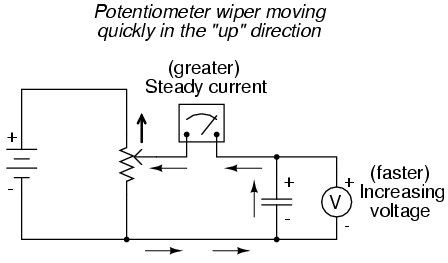
If the potentiometer is moved in the same direction, but at a faster rate, the rate of voltage change (dv/dt) will be greater and so will be the capacitor's current:

When mathematics students first study calculus, they begin by exploring the concept of rates of change for various mathematical functions. The derivative, which is the first and most elementary calculus principle, is an expression of one variable's rate of change in terms of another. Calculus students have to learn this principle while studying abstract equations. You get to learn this principle while studying something you can relate to: electric circuits!

To put this relationship between voltage and current in a capacitor in calculus terms, the current through a capacitor is the derivative of the voltage across the capacitor with respect to time. Or, stated in simpler terms, a capacitor's current is directly proportional to how quickly the voltage across it is changing. In this circuit where capacitor voltage is set by the position of a rotary knob on a potentiometer, we can say that the capacitor's current is directly proportional to how quickly we turn the knob.

If we to move the potentiometer's wiper in the same direction as before ("up"), but at varying rates, we would obtain graphs that looked like this:

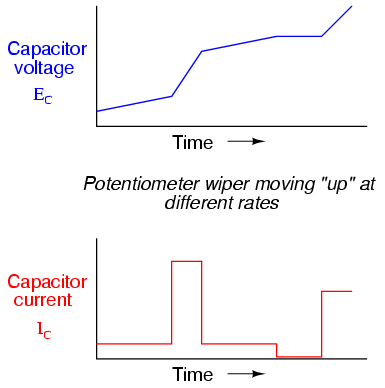
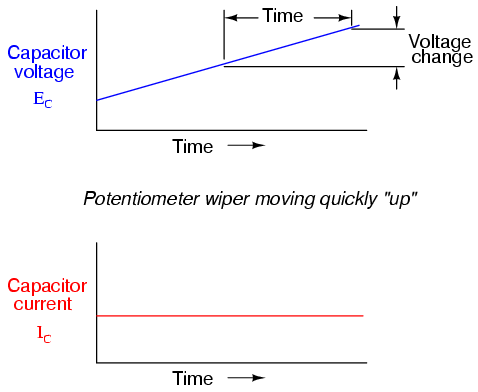
Note how that at any given point in time, the capacitor's current is proportional to the rate-of-change, or slope of the capacitor's voltage plot. When the voltage plot line is rising quickly (steep slope), the current will likewise be great. Where the voltage plot has a mild slope, the current is small. At one place in the voltage plot where it levels off (zero slope, representing a period of time when the potentiometer wasn't moving), the current falls to zero.

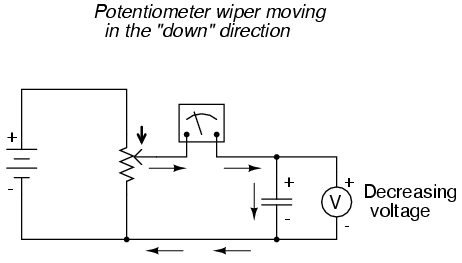
If we were to move the potentiometer wiper in the "down" direction, the capacitor voltage would decrease rather than increase. Again, the capacitor will react to this change of voltage by producing a current, but this time the current will be in the opposite direction. A decreasing capacitor voltage requires that the charge differential between the capacitor's plates be reduced, and that only way that can happen is if the electrons reverse their direction of flow, the capacitor discharging rather than charging. In this condition, with electrons exiting the negative plate and entering the positive, the capacitor will act as a source, like a battery, releasing its stored energy to the rest of the circuit.

Again, the amount of current through the capacitor is directly proportional to the rate of voltage change across it. The only difference between the effects of a decreasing voltage and an increasing voltage is the direction of electron flow. For the same rate of voltage change over time, either increasing or decreasing, the current magnitude (amps) will be the same. Mathematically, a decreasing voltage rate-of-change is expressed as a negative dv/dt quantity. Following the formula i = C(dv/dt), this will result in a current figure (i) that is likewise negative in sign, indicating a direction of flow corresponding to discharge of the capacitor.