Series and parallel inductors
When inductors are connected in series, the
total inductance is the sum of the individual inductors'
inductances. To understand why this is so, consider the
following: the definitive measure of inductance is the
amount of voltage dropped across an inductor for a given
rate of current change through it. If inductors are
connected together in series (thus sharing the same current,
and seeing the same rate of change in current), then the
total voltage dropped as the result of a change in current
will be additive with each inductor, creating a greater
total voltage than either of the individual inductors alone.
Greater voltage for the same rate of change in current means
greater inductance.
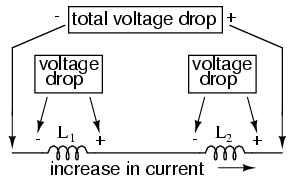
Thus, the total inductance for series
inductors is more than any one of the individual inductors'
inductances. The formula for calculating the series total
inductance is the same form as for calculating series
resistances:

When inductors are connected in parallel,
the total inductance is less than any one of the parallel
inductors' inductances. Again, remember that the definitive
measure of inductance is the amount of voltage dropped
across an inductor for a given rate of current change
through it. Since the current through each parallel inductor
will be a fraction of the total current, and the voltage
across each parallel inductor will be equal, a change in
total current will result in less voltage dropped across the
parallel array than for any one of the inductors considered
separately. In other words, there will be less voltage
dropped across parallel inductors for a given rate of change
in current than for any of of those inductors considered
separately, because total current divides among parallel
branches. Less voltage for the same rate of change in
current means less inductance.

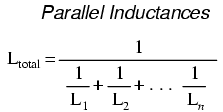
Thus, the total inductance is less than any
one of the individual inductors' inductances. The formula
for calculating the parallel total inductance is the same
form as for calculating parallel resistances:
|