Low-pass filters

By definition, a low-pass filter is a circuit offering easy passage to low-frequency signals and difficult passage to high-frequency signals. There are two basic kinds of circuits capable of accomplishing this objective, and many variations of each one:

The inductor's impedance increases with increasing frequency. This high impedance in series tends to block high-frequency signals from getting to the load. This can be demonstrated with a SPICE analysis:

inductive lowpass filter               
v1 1 0 ac 1 sin 
l1 1 2 3
rload 2 0 1k    
.ac lin 20 1 200
.plot ac v(2)   
.end    

freq       v(2)    0.2512      0.3981        0.631          1
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -  
1.000E+00  9.998E-01 .            .            .            * 
1.147E+01  9.774E-01 .            .            .           *.
2.195E+01  9.240E-01 .            .            .          * . 
3.242E+01  8.533E-01 .            .            .       *    .
4.289E+01  7.776E-01 .            .            .     *      .  
5.337E+01  7.050E-01 .            .            .  *         .  
6.384E+01  6.391E-01 .            .            *            .  
7.432E+01  5.810E-01 .            .         *  .            . 
8.479E+01  5.304E-01 .            .        *   .            .  
9.526E+01  4.865E-01 .            .     *      .            .   
1.057E+02  4.485E-01 .            .   *        .            .   
1.162E+02  4.153E-01 .            .*           .            .   
1.267E+02  3.863E-01 .           *.            .            .   
1.372E+02  3.607E-01 .         *  .            .            .   
1.476E+02  3.382E-01 .        *   .            .            .   
1.581E+02  3.181E-01 .      *     .            .            .   
1.686E+02  3.002E-01 .    *       .            .            .  
1.791E+02  2.841E-01 .   *        .            .            . 
1.895E+02  2.696E-01 . *          .            .            .  
2.000E+02  2.564E-01 .*           .            .            . 
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
Load voltage decreases with increasing frequency

The capacitor's impedance decreases with increasing frequency. This low impedance in parallel with the load resistance tends to short out high-frequency signals, dropping most of the voltage gets across series resistor R₁.

capacitive lowpass filter                                  
v1 1 0 ac 1 sin 
r1 1 2 500      
c1 2 0 7u       
rload 2 0 1k    
.ac lin 20 30 150       
.plot ac v(2)   
.end    

freq       v(2)            0.3162     0.3981     0.5012  0.631
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
3.000E+01  6.102E-01 .        .         .         .        *.
3.632E+01  5.885E-01 .        .         .         .      *  .
4.263E+01  5.653E-01 .        .         .         .   *     .
4.895E+01  5.416E-01 .        .         .         .  *      .
5.526E+01  5.180E-01 .        .         .         .*        .
6.158E+01  4.948E-01 .        .         .        *.         .
6.789E+01  4.725E-01 .        .         .     *   .         .
7.421E+01  4.511E-01 .        .         .   *     .         .
8.053E+01  4.309E-01 .        .         . *       .         .
8.684E+01  4.118E-01 .        .         .*        .         .
9.316E+01  3.938E-01 .        .        *.         .         .
9.947E+01  3.770E-01 .        .      *  .         .         .
1.058E+02  3.613E-01 .        .    *    .         .         .
1.121E+02  3.465E-01 .        .  *      .         .         .
1.184E+02  3.327E-01 .        .*        .         .         .
1.247E+02  3.199E-01 .        *         .         .         .
1.311E+02  3.078E-01 .      * .         .         .         .
1.374E+02  2.965E-01 .    *   .         .         .         .
1.437E+02  2.859E-01 .  *     .         .         .         .
1.500E+02  2.760E-01 .*       .         .         .         .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
                     Load voltage decreases with increasing frequency

The inductive low-pass filter is the pinnacle of simplicity, with only one component comprising the filter. The capacitive version of this filter is not that much more complex, with only a resistor and capacitor needed for operation. However, despite their increased complexity, capacitive filter designs are generally preferred over inductive because capacitors tend to be "purer" reactive components than inductors and therefore are more predictable in their behavior. By "pure" I mean that capacitors exhibit little resistive effects than inductors, making them almost 100% reactive. Inductors, on the other hand, typically exhibit significant dissipative (resistor-like) effects, both in the long lengths of wire used to make them, and in the magnetic losses of the core material. Capacitors also tend to participate less in "coupling" effects with other components (generate and/or receive interference from other components via mutual electric or magnetic fields) than inductors, and are less expensive.

However, the inductive low-pass filter is often preferred in AC-DC power supplies to filter out the AC "ripple" waveform created when AC is converted (rectified) into DC, passing only the pure DC component. The primary reason for this is the requirement of low filter resistance for the output of such a power supply. A capacitive low-pass filter requires an extra resistance in series with the source, whereas the inductive low-pass filter does not. In the design of a high-current circuit like a DC power supply where additional series resistance is undesirable, the inductive low-pass filter is the better design choice. On the other hand, if low weight and compact size are higher priorities than low internal supply resistance in a power supply design, the capacitive low-pass filter might make more sense.

All low-pass filters are rated at a certain cutoff frequency. That is, the frequency above which the output voltage falls below 70.7% of the input voltage. This cutoff percentage of 70.7 is not really arbitrary, all though it may seem so at first glance. In a simple capacitive/resistive low-pass filter, it is the frequency at which capacitive reactance in ohms equals resistance in ohms. In a simple capacitive low-pass filter (one resistor, one capacitor), the cutoff frequency is given as:

Inserting the values of R and C from the last SPICE simulation into this formula, we arrive at a cutoff frequency of 45.473 Hz. However, when we look at the plot generated by the SPICE simulation, we see the load voltage well below 70.7% of the source voltage (1 volt) even at a frequency as low as 30 Hz, below the calculated cutoff point. What's wrong? The problem here is that the load resistance of 1 kΩ affects the frequency response of the filter, skewing it down from what the formula told us it would be. Without that load resistance in place, SPICE produces a Bode plot whose numbers make more sense:

capacitive lowpass filter   
v1 1 0 ac 1 sin 
r1 1 2 500      
c1 2 0 7u
* note: no load resistor!       
.ac lin 20 40 50
.plot ac v(2)   
.end    

freq       v(2)    0.6607      0.6918       0.7244       0.7586
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
4.000E+01  7.508E-01 .           .             .          *  . 
4.053E+01  7.465E-01 .           .             .        *    .
4.105E+01  7.423E-01 .           .             .      *      . 
4.158E+01  7.380E-01 .           .             .     *       .
4.211E+01  7.338E-01 .           .             .   *         . 
4.263E+01  7.295E-01 .           .             . *           .
4.316E+01  7.253E-01 .           .             *             . 
4.368E+01  7.211E-01 .           .            *.             .
4.421E+01  7.170E-01 .           .          *  .             .
4.474E+01  7.129E-01 .           .        *    .             .
4.526E+01  7.087E-01 .           .      *      .             .
4.579E+01  7.046E-01 .           .     *       .             .
4.632E+01  7.006E-01 .           .   *         .             .
4.684E+01  6.965E-01 .           . *           .             .
4.737E+01  6.925E-01 .           *             .             .
4.789E+01  6.885E-01 .          *.             .             .
4.842E+01  6.846E-01 .        *  .             .             .
4.895E+01  6.806E-01 .      *    .             .             .
4.947E+01  6.767E-01 .    *      .             .             .
5.000E+01  6.728E-01 .   *       .             .             .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 
At 45.26 Hz, the output voltage is above 70.7 percent;
At 45.79 Hz, the output voltage is below 70.7 percent;
It should be exactly 70.7% at 45.473 Hz!

When dealing with filter circuits, it is always important to note that the response of the filter depends on the filter's component values and the impedance of the load. If a cutoff frequency equation fails to give consideration to load impedance, it assumes no load and will fail to give accurate results for a real-life filter conducting power to a load.

One frequent application of the capacitive low-pass filter principle is in the design of circuits having components or sections sensitive to electrical "noise." As mentioned at the beginning of the last chapter, sometimes AC signals can "couple" from one circuit to another via capacitance (C_stray) and/or mutual inductance (M_stray) between the two sets of conductors. A prime example of this is unwanted AC signals ("noise") becoming impressed on DC power lines supplying sensitive circuits:

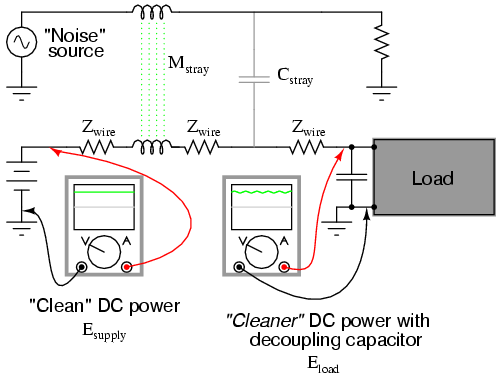
The oscilloscope-meter on the left shows the "clean" power from the DC voltage source. After coupling with the AC noise source via stray mutual inductance and stray capacitance, though, the voltage as measured at the load terminals is now a mix of AC and DC, the AC being unwanted. Normally, one would expect E_load to be precisely identical to E_source, because the uninterrupted conductors connecting them should make the two sets of points electrically common. However, power conductor impedance allows the two voltages to differ, which means the noise magnitude can vary at different points in the DC system.

If we wish to prevent such "noise" from reaching the DC load, all we need to do is connect a low-pass filter near the load to block any coupled signals. In its simplest form, this is nothing more than a capacitor connected directly across the power terminals of the load, the capacitor behaving as a very low impedance to any AC noise, and shorting it out. Such a capacitor is called a decoupling capacitor:

A cursory glance at a crowded printed-circuit board (PCB) will typically reveal decoupling capacitors scattered throughout, usually located as close as possible to the sensitive DC loads. Capacitor size is usually 0.1 �F or more, a minimum amount of capacitance needed to produce a low enough impedance to short out any noise. Greater capacitance will do a better job at filtering noise, but size and economics limit decoupling capacitors to meager values.

• REVIEW:

• A low-pass filter allows for easy passage of low-frequency signals from source to load, and difficult passage of high-frequency signals.

• Inductive low-pass filters insert an inductor in series with the load; capacitive low-pass filters insert a resistor in series and a capacitor in parallel with the load. The former filter design tries to "block" the unwanted frequency signal while the latter tries to short it out.

• The cutoff frequency for a low-pass filter is that frequency at which the output (load) voltage equals 70.7% of the input (source) voltage. Above the cutoff frequency, the output voltage is lower than 70.7% of the input, and visa-versa.