Practical power factor correction

When the need arises to correct for poor power factor in an AC power system, you probably won't have the luxury of knowing the load's exact inductance in henrys to use for your calculations. You may be fortunate enough to have an instrument called a power factor meter to tell you what the power factor is (a number between 0 and 1), and the apparent power (which can be figured by taking a voltmeter reading in volts and multiplying by an ammeter reading in amps). In less favorable circumstances you may have to use an oscilloscope to compare voltage and current waveforms, measuring phase shift in degrees and calculating power factor by the cosine of that phase shift.

Most likely, you will have access to a wattmeter for measuring true power, whose reading you can compare against a calculation of apparent power (from multiplying total voltage and total current measurements). From the values of true and apparent power, you can determine reactive power and power factor. Let's do an example problem to see how this works:

First, we need to calculate the apparent power in kVA. We can do this by multiplying load voltage by load current:

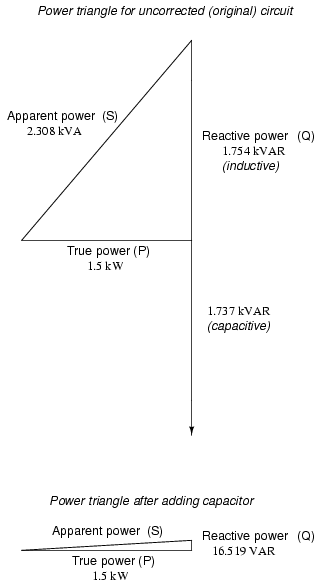
As we can see, 2.308 kVA is a much larger figure than 1.5 kW, which tells us that the power factor in this circuit is rather poor (substantially less than 1). Now, we figure the power factor of this load by dividing the true power by the apparent power:

Using this value for power factor, we can draw a power triangle, and from that determine the reactive power of this load:

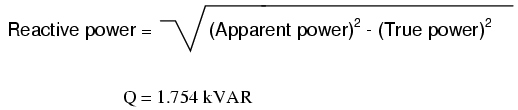
To determine the unknown (reactive power) triangle quantity, we use the Pythagorean Theorem "backwards," given the length of the hypotenuse (apparent power) and the length of the adjacent side (true power):

If this load is an electric motor, or most any other industrial AC load, it will have a lagging (inductive) power factor, which means that we'll have to correct for it with a capacitor of appropriate size, wired in parallel. Now that we know the amount of reactive power (1.754 kVAR), we can calculate the size of capacitor needed to counteract its effects:

Rounding this answer off to 80 �F, we can place that size of capacitor in the circuit and calculate the results:

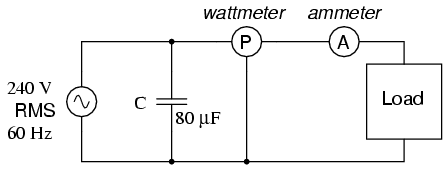
An 80 �F capacitor will have a capacitive reactance of 33.157 Ω, giving a current of 7.238 amps, and a corresponding reactive power of 1.737 kVAR (for the capacitor only). Since the capacitor's current is 180^o out of phase from the the load's inductive contribution to current draw, the capacitor's reactive power will directly subtract from the load's reactive power, resulting in:

This correction, of course, will not change the amount of true power consumed by the load, but it will result in a substantial reduction of apparent power, and of the total current drawn from the 240 Volt source:

The new apparent power can be found from the true and new reactive power values, using the standard form of the Pythagorean Theorem:

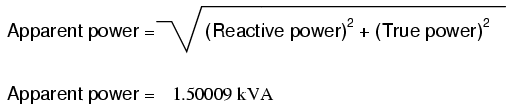
This gives a corrected power factor of (1.5kW / 1.5009 kVA), or 0.99994, and a new total current of (1.50009 kVA / 240 Volts), or 6.25 amps, a substantial improvement over the uncorrected value of 9.615 amps! This lower total current will translate to less heat losses in the circuit wiring, meaning greater system efficiency (less power wasted).