In mathematics, an identity is a statement true for all possible values of its variable or variables. The algebraic identity of x + 0 = x tells us that anything (x) added to zero equals the original "anything," no matter what value that "anything" (x) may be. Like ordinary algebra, Boolean algebra has its own unique identities based on the bivalent states of Boolean variables.

The first Boolean identity is that the sum of anything and zero is the same as the original "anything." This identity is no different from its real-number algebraic equivalent:

No matter what the value of A, the output will always be the same: when A=1, the output will also be 1; when A=0, the output will also be 0.

The next identity is most definitely different from any seen in normal algebra. Here we discover that the sum of anything and one is one:

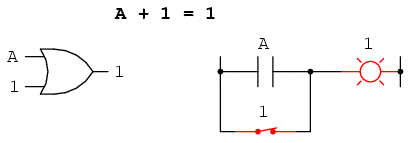
No matter what the value of A, the sum of A and 1 will always be 1. In a sense, the "1" signal overrides the effect of A on the logic circuit, leaving the output fixed at a logic level of 1.

Next, we examine the effect of adding A and A together, which is the same as connecting both inputs of an OR gate to each other and activating them with the same signal:

In real-number algebra, the sum of two identical variables is twice the original variable's value (x + x = 2x), but remember that there is no concept of "2" in the world of Boolean math, only 1 and 0, so we cannot say that A + A = 2A. Thus, when we add a Boolean quantity to itself, the sum is equal to the original quantity: 0 + 0 = 0, and 1 + 1 = 1.

Introducing the uniquely Boolean concept of complementation into an additive identity, we find an interesting effect. Since there must be one "1" value between any variable and its complement, and since the sum of any Boolean quantity and 1 is 1, the sum of a variable and its complement must be 1:

Just as there are four Boolean additive identities (A+0, A+1, A+A, and A+A'), so there are also four multiplicative identities: Ax0, Ax1, AxA, and AxA'. Of these, the first two are no different from their equivalent expressions in regular algebra:

The third multiplicative identity expresses the result of a Boolean quantity multiplied by itself. In normal algebra, the product of a variable and itself is the square of that variable (3 x 3 = 3² = 9). However, the concept of "square" implies a quantity of 2, which has no meaning in Boolean algebra, so we cannot say that A x A = A². Instead, we find that the product of a Boolean quantity and itself is the original quantity, since 0 x 0 = 0 and 1 x 1 = 1:

The fourth multiplicative identity has no equivalent in regular algebra because it uses the complement of a variable, a concept unique to Boolean mathematics. Since there must be one "0" value between any variable and its complement, and since the product of any Boolean quantity and 0 is 0, the product of a variable and its complement must be 0:

To summarize, then, we have four basic Boolean identities for addition and four for multiplication:

Another identity having to do with complementation is that of the double complement: a variable inverted twice. Complementing a variable twice (or any even number of times) results in the original Boolean value. This is analogous to negating (multiplying by -1) in real-number algebra: an even number of negations cancel to leave the original value: