Suppose we wanted to build a device that could
add two binary bits together. Such a device is known as a half-adder, and
its gate circuit looks like this:
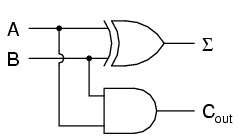
The Σ symbol represents the "sum" output of the half-adder, the sum's
least significant bit (LSB). Cout represents the "carry" output
of the half-adder, the sum's most significant bit (MSB).
If we were to implement this same function in ladder (relay) logic, it
would look like this:
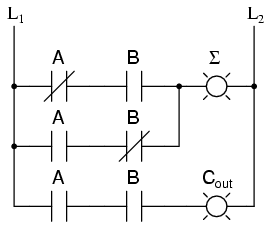
Either circuit is capable of adding two binary digits together. The
mathematical "rules" of how to add bits together are intrinsic to the
hard-wired logic of the circuits. If we wanted to perform a different
arithmetic operation with binary bits, such as multiplication, we would have
to construct another circuit. The above circuit designs will only perform
one function: add two binary bits together. To make them do something else
would take re-wiring, and perhaps different componentry.
In this sense, digital arithmetic circuits aren't much different from
analog arithmetic (operational amplifier) circuits: they do exactly what
they're wired to do, no more and no less. We are not, however, restricted to
designing digital computer circuits in this manner. It is possible to embed
the mathematical "rules" for any arithmetic operation in the form of digital
data rather than in hard-wired connections between gates. The result is
unparalleled flexibility in operation, giving rise to a whole new kind of
digital device: the programmable computer.
While this chapter is by no means exhaustive, it provides what I believe
is a unique and interesting look at the nature of programmable computer
devices, starting with two devices often overlooked in introductory
textbooks: look-up table memories and finite-state machines. |