Correct use of Ohm's Law

One of the most common mistakes made by beginning electronics students in their application of Ohm's Laws is mixing the contexts of voltage, current, and resistance. In other words, a student might mistakenly use a value for I through one resistor and the value for E across a set of interconnected resistors, thinking that they'll arrive at the resistance of that one resistor. Not so! Remember this important rule: The variables used in Ohm's Law equations must be common to the same two points in the circuit under consideration. I cannot overemphasize this rule. This is especially important in series-parallel combination circuits where nearby components may have different values for both voltage drop and current.

When using Ohm's Law to calculate a variable pertaining to a single component, be sure the voltage you're referencing is solely across that single component and the current you're referencing is solely through that single component and the resistance you're referencing is solely for that single component. Likewise, when calculating a variable pertaining to a set of components in a circuit, be sure that the voltage, current, and resistance values are specific to that complete set of components only! A good way to remember this is to pay close attention to the two points terminating the component or set of components being analyzed, making sure that the voltage in question is across those two points, that the current in question is the electron flow from one of those points all the way to the other point, that the resistance in question is the equivalent of a single resistor between those two points, and that the power in question is the total power dissipated by all components between those two points.

The "table" method presented for both series and parallel circuits in this chapter is a good way to keep the context of Ohm's Law correct for any kind of circuit configuration. In a table like the one shown below, you are only allowed to apply an Ohm's Law equation for the values of a single vertical column at a time:

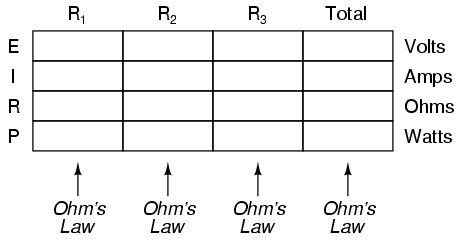
Deriving values horizontally across columns is allowable as per the principles of series and parallel circuits:

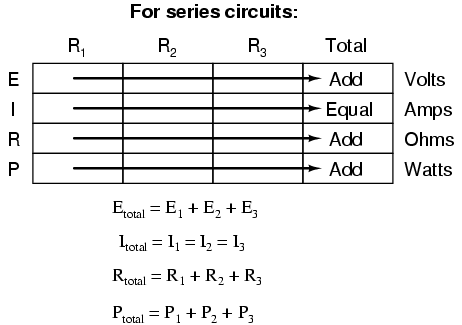
Not only does the "table" method simplify the management of all relevant quantities, it also facilitates cross-checking of answers by making it easy to solve for the original unknown variables through other methods, or by working backwards to solve for the initially given values from your solutions. For example, if you have just solved for all unknown voltages, currents, and resistances in a circuit, you can check your work by adding a row at the bottom for power calculations on each resistor, seeing whether or not all the individual power values add up to the total power. If not, then you must have made a mistake somewhere! While this technique of "cross-checking" your work is nothing new, using the table to arrange all the data for the cross-check(s) results in a minimum of confusion.

• REVIEW:

• Apply Ohm's Law to vertical columns in the table.

• Apply rules of series/parallel to horizontal rows in the table.

• Check your calculations by working "backwards" to try to arrive at originally given values (from your first calculated answers), or by solving for a quantity using more than one method (from different given values).