More on AC "polarity"
Complex numbers are useful for AC circuit
analysis because they provide a convenient method of
symbolically denoting phase shift between AC quantities like
voltage and current. However, for most people the
equivalence between abstract vectors and real circuit
quantities is not an easy one to grasp. Earlier in this
chapter we saw how AC voltage sources are given voltage
figures in complex form (magnitude and phase angle),
as well as polarity markings. Being that alternating current
has no set "polarity" as direct current does, these polarity
markings and their relationship to phase angle tends to be
confusing. This section is written in the attempt to clarify
some of these issues.
Voltage is an inherently relative
quantity. When we measure a voltage, we have a choice in how
we connect a voltmeter or other voltage-measuring instrument
to the source of voltage, as there are two points between
which the voltage exists, and two test leads on the
instrument with which to make connection. In DC circuits, we
denote the polarity of voltage sources and voltage drops
explicitly, using "+" and "-" symbols, and use color-coded
meter test leads (red and black). If a digital voltmeter
indicates a negative DC voltage, we know that its test leads
are connected "backward" to the voltage (red lead connected
to the "-" and black lead to the "+").
Batteries have their polarity designated by
way of intrinsic symbology: the short-line side of a battery
is always the negative (-) side and the long-line side
always the positive (+):

Although it would be mathematically correct
to represent a battery's voltage as a negative figure with
reversed polarity markings, it would be decidedly
unconventional:
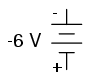
Interpreting such notation might be easier
if the "+" and "-" polarity markings were viewed as
reference points for voltmeter test leads, the "+" meaning
"red" and the "-" meaning "black." A voltmeter connected to
the above battery with red lead to the bottom terminal and
black lead to the top terminal would indeed indicate a
negative voltage (-6 volts). Actually, this form of notation
and interpretation is not as unusual as you might think:
it's commonly encountered in problems of DC network analysis
where "+" and "-" polarity marks are initially drawn
according to educated guess, and later interpreted as
correct or "backward" according to the mathematical sign of
the figure calculated.
In AC circuits, though, we don't deal with
"negative" quantities of voltage. Instead, we describe to
what degree one voltage aids or opposes another by phase:
the time-shift between two waveforms. We never describe an
AC voltage as being negative in sign, because the facility
of polar notation allows for vectors pointing in an opposite
direction. If one AC voltage directly opposes another AC
voltage, we simply say that one is 180o out of
phase with the other.
Still, voltage is relative between two
points, and we have a choice in how we might connect a
voltage-measuring instrument between those two points. The
mathematical sign of a DC voltmeter's reading has meaning
only in the context of its test lead connections: which
terminal the red lead is touching, and which terminal the
black lead is touching. Likewise, the phase angle of an AC
voltage has meaning only in the context of knowing which of
the two points is considered the "reference" point. Because
of this fact, "+" and "-" polarity marks are often placed by
the terminals of an AC voltage in schematic diagrams to give
the stated phase angle a frame of reference.
Let's review these principles with some
graphical aids. First, the principle of relating test lead
connections to the mathematical sign of a DC voltmeter
indication:

The mathematical sign of a digital DC
voltmeter's display has meaning only in the context of its
test lead connections. Consider the use of a DC voltmeter in
determining whether or not two DC voltage sources are aiding
or opposing each other, assuming that both sources are
unlabeled as to their polarities. Using the voltmeter to
measure across the first source:

This first measurement of +24 across the
left-hand voltage source tells us that the black lead of the
meter really is touching the negative side of voltage source
#1, and the red lead of the meter really is touching the
positive. Thus, we know source #1 is a battery facing in
this orientation:

Measuring the other unknown voltage source:

This second voltmeter reading, however, is a
negative (-) 17 volts, which tells us that the black
test lead is actually touching the positive side of voltage
source #2, while the red test lead is actually touching the
negative. Thus, we know that source #2 is a battery facing
in the opposite direction:

It should be obvious to any experienced
student of DC electricity that these two batteries are
opposing one another. By definition, opposing voltages
subtract from one another, so we subtract 17 volts from
24 volts to obtain the total voltage across the two: 7
volts.
We could, however, draw the two sources as
nondescript boxes, labeled with the exact voltage figures
obtained by the voltmeter, the polarity marks indicating
voltmeter test lead placement:

According to this diagram, the polarity
marks (which indicate meter test lead placement) indicate
the sources aiding each other. By definition, aiding
voltage sources add with one another to form the
total voltage, so we add 24 volts to -17 volts to obtain 7
volts: still the correct answer. If we let the polarity
markings guide our decision to either add or subtract
voltage figures -- whether those polarity markings represent
the true polarity or just the meter test lead
orientation -- and include the mathematical signs of those
voltage figures in our calculations, the result will always
be correct. Again, the polarity markings serve as frames
of reference to place the voltage figures' mathematical
signs in proper context.
The same is true for AC voltages, except
that phase angle substitutes for mathematical sign.
In order to relate multiple AC voltages at different phase
angles to each other, we need polarity markings to provide
frames of reference for those voltages' phase angles.
Take for example the following circuit:

The polarity markings show these two voltage
sources aiding each other, so to determine the total voltage
across the resistor we must add the voltage figures
of 10 V ∠ 0o and 6 V ∠ 45o together to
obtain 14.861 V ∠ 16.59o. However, it would be
perfectly acceptable to represent the 6 volt source as 6 V ∠
225o, with a reversed set of polarity markings,
and still arrive at the same total voltage:

6 V ∠ 45o with negative on the
left and positive on the right is exactly the same as 6 V ∠
225o with positive on the left and negative on
the right: the reversal of polarity markings perfectly
complements the addition of 180o to the phase
angle designation:

Unlike DC voltage sources, whose symbols
intrinsically define polarity by means of short and long
lines, AC voltage symbols have no intrinsic polarity
marking. Therefore, any polarity marks must by included as
additional symbols on the diagram, and there is no one
"correct" way in which to place them. They must, however,
correlate with the given phase angle to represent the true
phase relationship of that voltage with other voltages in
the circuit.
|