Polar and rectangular notation

In order to work with these complex numbers without drawing vectors, we first need some kind of standard mathematical notation. There are two basic forms of complex number notation: polar and rectangular.

Polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or modulus) and the angle of its vector (usually denoted by an angle symbol that looks like this: ∠). To use the map analogy, polar notation for the vector from New York City to San Diego would be something like "2400 miles, southwest." Here are two examples of vectors and their polar notations:

Standard orientation for vector angles in AC circuit calculations defines 0^o as being to the right (horizontal), making 90^o straight up, 180^o to the left, and 270^o straight down. Please note that vectors angled "down" can have angles represented in polar form as positive numbers in excess of 180, or negative numbers less than 180. For example, a vector angled ∠ 270^o (straight down) can also be said to have an angle of -90^o. The above vector on the right (5.4 ∠ 326^o) can also be denoted as 5.4 ∠ -34^o.

Rectangular form, on the other hand, is where a complex number is denoted by its respective horizontal and vertical components. In essence, the angled vector is taken to be the hypotenuse of a right triangle, described by the lengths of the adjacent and opposite sides. Rather than describing a vector's length and direction by denoting magnitude and angle, it is described in terms of "how far left/right" and "how far up/down."

These two dimensional figures (horizontal and vertical) are symbolized by two numerical figures. In order to distinguish the horizontal and vertical dimensions from each other, the vertical is prefixed with a lower-case "i" (in pure mathematics) or "j" (in electronics). These lower-case letters do not represent a physical variable (such as instantaneous current, also symbolized by a lower-case letter "i"), but rather are mathematical operators used to distinguish the vector's vertical component from its horizontal component. As a complete complex number, the horizontal and vertical quantities are written as a sum:

The horizontal component is referred to as the real component, since that dimension is compatible with normal, scalar ("real") numbers. The vertical component is referred to as the imaginary component, since that dimension lies in a different direction, totally alien to the scale of the real numbers.

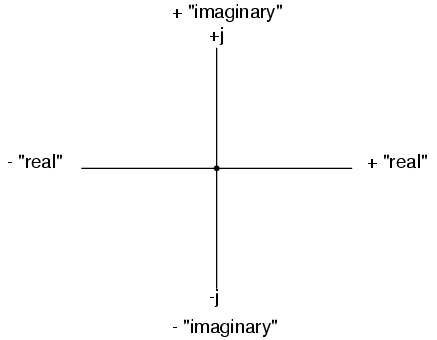
The "real" axis of the graph corresponds to the familiar number line we saw earlier: the one with both positive and negative values on it. The "imaginary" axis of the graph corresponds to another number line situated at 90^o to the "real" one. Vectors being two-dimensional things, we must have a two-dimensional "map" upon which to express them, thus the two number lines perpendicular to each other:

Either method of notation is valid for complex numbers. The primary reason for having two methods of notation is for ease of longhand calculation, rectangular form lending itself to addition and subtraction, and polar form lending itself to multiplication and division.

Conversion between the two notational forms involves simple trigonometry. To convert from polar to rectangular, find the real component by multiplying the polar magnitude by the cosine of the angle, and the imaginary component by multiplying the polar magnitude by the sine of the angle. This may be understood more readily by drawing the quantities as sides of a right triangle, the hypotenuse of the triangle representing the vector itself (its length and angle with respect to the horizontal constituting the polar form), the horizontal and vertical sides representing the "real" and "imaginary" rectangular components, respectively:

To convert from rectangular to polar, find the polar magnitude through the use of the Pythagorean Theorem (the polar magnitude is the hypotenuse of a right triangle, and the real and imaginary components are the adjacent and opposite sides, respectively), and the angle by taking the arctangent of the imaginary component divided by the real component:

• REVIEW:

• Polar notation denotes a complex number in terms of its vector's length and angular direction from the starting point. Example: fly 45 miles ∠ 203^o (West by Southwest).

• Rectangular notation denotes a complex number in terms of its horizontal and vertical dimensions. Example: drive 41 miles West, then turn and drive 18 miles South.

• In rectangular notation, the first quantity is the "real" component (horizontal dimension of vector) and the second quantity is the "imaginary" component (vertical dimension of vector). The imaginary component is preceded by a lower-case "j," sometimes called the j operator.

• Both polar and rectangular forms of notation for a complex number can be related graphically in the form of a right triangle, with the hypotenuse representing the vector itself (polar form: hypotenuse length = magnitude; angle with respect to horizontal side = angle), the horizontal side representing the rectangular "real" component, and the vertical side representing the rectangular "imaginary" component.