Simple vector addition

Remember that vectors are mathematical objects just like numbers on a number line: they can be added, subtracted, multiplied, and divided. Addition is perhaps the easiest vector operation to visualize, so we'll begin with that. If vectors with common angles are added, their magnitudes (lengths) add up just like regular scalar quantities:

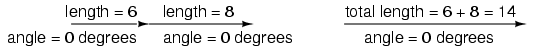
Similarly, if AC voltage sources with the same phase angle are connected together in series, their voltages add just as you might expect with DC batteries:

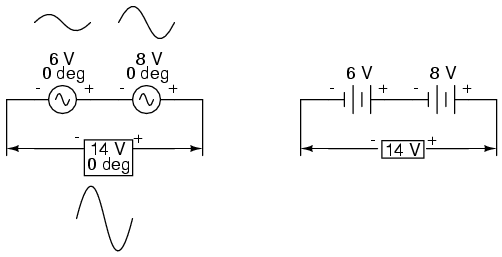
Please note the (+) and (-) polarity marks next to the leads of the two AC sources. Even though we know AC doesn't have "polarity" in the same sense that DC does, these marks are essential to knowing how to reference the given phase angles of the voltages. This will become more apparent in the next example.

If vectors directly opposing each other (180^o out of phase) are added together, their magnitudes (lengths) subtract just like positive and negative scalar quantities subtract when added:

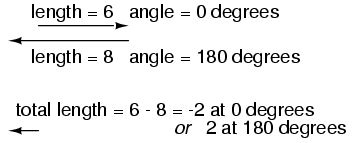
Similarly, if opposing AC voltage sources are connected in series, their voltages subtract as you might expect with DC batteries connected in an opposing fashion:

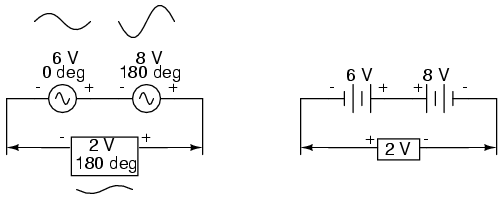
Determining whether or not these voltage sources are opposing each other requires an examination of their polarity markings and their phase angles. Notice how the polarity markings in the above diagram seem to indicate additive voltages (from left to right, we see - and + on the 6 volt source, - and + on the 8 volt source). Even though these polarity markings would normally indicate an additive effect in a DC circuit (the two voltages working together to produce a greater total voltage), in this AC circuit they're actually pushing in opposite directions because one of those voltages has a phase angle of 0^o and the other a phase angle of 180^o. The result, of course, is a total voltage of 2 volts.

We could have just as well shown the opposing voltages subtracting in series like this:

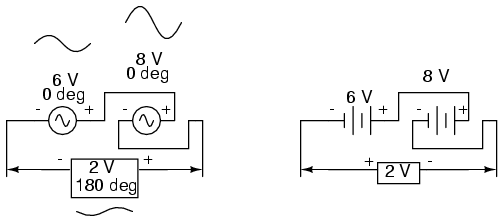
Note how the polarities appear to be opposed to each other now, due to the reversal of wire connections on the 8 volt source. Since both sources are described as having equal phase angles (0^o), they truly are opposed to one another, and the overall effect is the same as the former scenario with "additive" polarities and differing phase angles: a total voltage of only 2 volts.

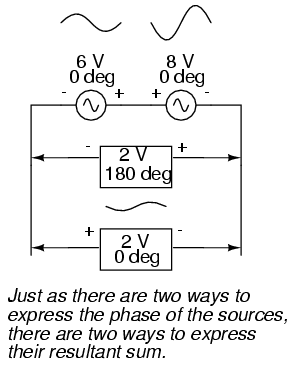
The resultant voltage can be expressed in two different ways: 2 volts at 180^o with the (-) symbol on the left and the (+) symbol on the right, or 2 volts at 0^o with the (+) symbol on the left and the (-) symbol on the right. A reversal of wires from an AC voltage source is the same as phase-shifting that source by 180^o.
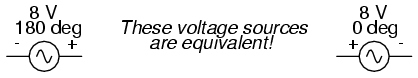