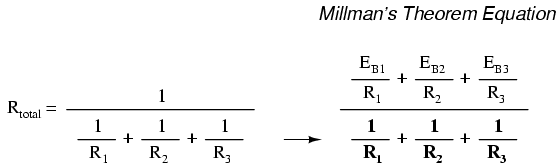
Millman's Theorem revisited

You may have wondered where we got that strange equation for the determination of "Millman Voltage" across parallel branches of a circuit where each branch contains a series resistance and voltage source:

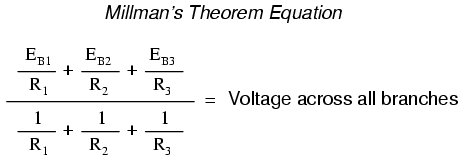
Parts of this equation seem familiar to equations we've seen before. For instance, the denominator of the large fraction looks conspicuously like the denominator of our parallel resistance equation. And, of course, the E/R terms in the numerator of the large fraction should give figures for current, Ohm's Law being what it is (I=E/R).

Now that we've covered Thevenin and Norton source equivalencies, we have the tools necessary to understand Millman's equation. What Millman's equation is actually doing is treating each branch (with its series voltage source and resistance) as a Thevenin equivalent circuit and then converting each one into equivalent Norton circuits.

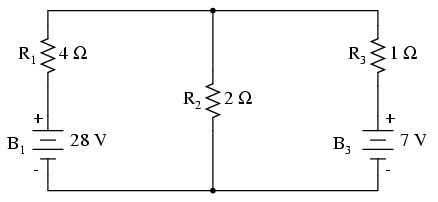
Thus, in the circuit above, battery B₁ and resistor R₁ are seen as a Thevenin source to be converted into a Norton source of 7 amps (28 volts / 4 Ω) in parallel with a 4 Ω resistor. The rightmost branch will be converted into a 7 amp current source (7 volts / 1 Ω) and 1 Ω resistor in parallel. The center branch, containing no voltage source at all, will be converted into a Norton source of 0 amps in parallel with a 2 Ω resistor:

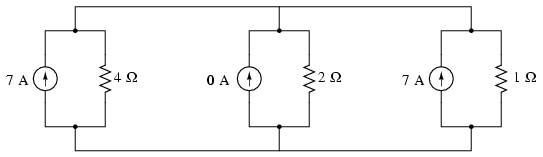
Since current sources directly add their respective currents in parallel, the total circuit current will be 7 + 0 + 7, or 14 amps. This addition of Norton source currents is what's being represented in the numerator of the Millman equation:

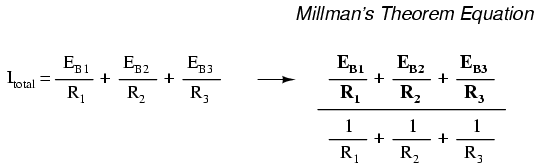
All the Norton resistances are in parallel with each other as well in the equivalent circuit, so they diminish to create a total resistance. This diminishing of source resistances is what's being represented in the denominator of the Millman's equation:

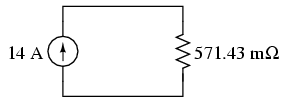
In this case, the resistance total will be equal to 571.43 milliohms (571.43 mΩ). We can re-draw our equivalent circuit now as one with a single Norton current source and Norton resistance:

Ohm's Law can tell us the voltage across these two components now (E=IR):

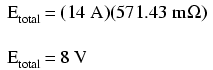
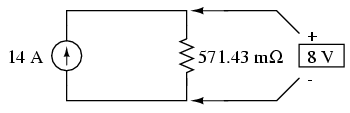
Let's summarize what we know about the circuit thus far. We know that the total current in this circuit is given by the sum of all the branch voltages divided by their respective currents. We also know that the total resistance is found by taking the reciprocal of all the branch resistance reciprocals. Furthermore, we should be well aware of the fact that total voltage across all the branches can be found by multiplying total current by total resistance (E=IR). All we need to do is put together the two equations we had earlier for total circuit current and total resistance, multiplying them to find total voltage:

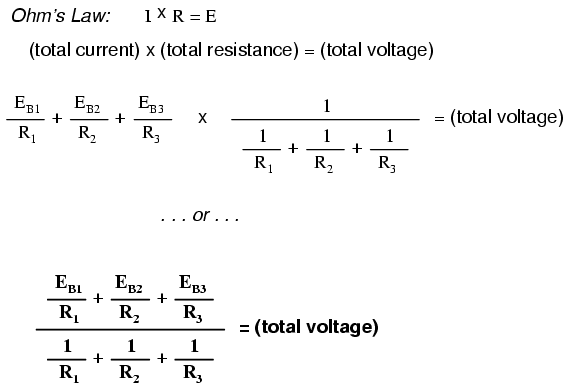
The Millman's equation is nothing more than a Thevenin-to-Norton conversion matched together with the parallel resistance formula to find total voltage across all the branches of the circuit. So, hopefully some of the mystery is gone now!