Other waveshapes
As strange as it may seem, any
repeating, non-sinusoidal waveform is actually equivalent to
a series of sinusoidal waveforms of different amplitudes and
frequencies added together. Square waves are a very common
and well-understood case, but not the only one.
Electronic power control devices such as
transistors and silicon-controlled rectifiers (SCRs)
often produce voltage and current waveforms that are
essentially chopped-up versions of the otherwise "clean"
(pure) sine-wave AC from the power supply. These devices
have the ability to suddenly change their resistance
with the application of a control signal voltage or current,
thus "turning on" or "turning off" almost instantaneously,
producing current waveforms bearing little resemblance to
the source voltage waveform powering the circuit. These
current waveforms then produce changes in the voltage
waveform to other circuit components, due to voltage drops
created by the non-sinusoidal current through circuit
impedances.
Circuit components that distort the normal
sine-wave shape of AC voltage or current are called
nonlinear. Nonlinear components such as SCRs find
popular use in power electronics due to their ability to
regulate large amounts of electrical power without
dissipating much heat. While this is an advantage from the
perspective of energy efficiency, the waveshape distortions
they introduce can cause problems.
These non-sinusoidal waveforms, regardless
of their actual shape, are equivalent to a series of
sinusoidal waveforms of higher (harmonic) frequencies. If
not taken into consideration by the circuit designer, these
harmonic waveforms created by electronic switching
components may cause erratic circuit behavior. It is
becoming increasingly common in the electric power industry
to observe overheating of transformers and motors due to
distortions in the sine-wave shape of the AC power line
voltage stemming from "switching" loads such as computers
and high-efficiency lights. This is no theoretical exercise:
it is very real and potentially very troublesome.
In this section, I will investigate a few of
the more common waveshapes and show their harmonic
components by way of Fourier analysis using SPICE.
One very common way harmonics are generated
in an AC power system is when AC is converted, or
"rectified" into DC. This is generally done with components
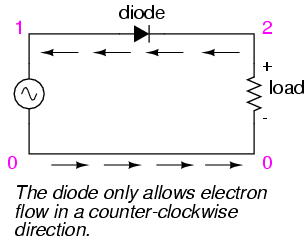
called diodes, which only allow passage current in
one direction. The simplest type of AC/DC rectification is
half-wave, where a single diode blocks half of the AC
current (over time) from passing through the load. Oddly
enough, the conventional diode schematic symbol is drawn
such that electrons flow against the direction of the
symbol's arrowhead:
halfwave rectifier
v1 1 0 sin(0 15 60 0 0)
rload 2 0 10k
d1 1 2 mod1
.model mod1 d
.tran .5m 17m
.plot tran v(1,0) v(2,0)
.four 60 v(1,0) v(2,0)
.end
legend:
*: v(1)
+: v(2)
time v(1)
(*)---------- -20 -10 0 10 20
(+)---------- -5 0 5 10 15
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 0.000E+00 . + * . .
5.000E-04 2.806E+00 . . + . * . .
1.000E-03 5.483E+00 . . + * . .
1.500E-03 7.929E+00 . . . + *. .
2.000E-03 1.013E+01 . . . +* .
2.500E-03 1.198E+01 . . . . *+ .
3.000E-03 1.338E+01 . . . . * + .
3.500E-03 1.435E+01 . . . . * + .
4.000E-03 1.476E+01 . . . . * +.
4.500E-03 1.470E+01 . . . . * +.
5.000E-03 1.406E+01 . . . . * + .
5.500E-03 1.299E+01 . . . . * + .
6.000E-03 1.139E+01 . . . . x .
6.500E-03 9.455E+00 . . . + *. .
7.000E-03 7.113E+00 . . . + * . .
7.500E-03 4.591E+00 . . + . * . .
8.000E-03 1.841E+00 . . + . * . .
8.500E-03 -9.177E-01 . + *. . .
9.000E-03 -3.689E+00 . + * . . .
9.500E-03 -6.298E+00 . + * . . .
1.000E-02 -8.701E+00 . +* . . .
1.050E-02 -1.079E+01 . *+ . . .
1.100E-02 -1.249E+01 . * + . . .
1.150E-02 -1.377E+01 . * + . . .
1.200E-02 -1.453E+01 . * + . . .
1.250E-02 -1.482E+01 .* + . . .
1.300E-02 -1.452E+01 . * + . . .
1.350E-02 -1.378E+01 . * + . . .
1.400E-02 -1.248E+01 . * + . . .
1.450E-02 -1.081E+01 . *+ . . .
1.500E-02 -8.681E+00 . +* . . .
1.550E-02 -6.321E+00 . + * . . .
1.600E-02 -3.666E+00 . + * . . .
1.650E-02 -9.432E-01 . . + *. . .
1.700E-02 1.865E+00 . . + . * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
First, we'll see how SPICE analyzes the
source waveform, a pure sine wave voltage:
fourier components of transient response v(1)
dc component = 8.016E-04
harmonic frequency fourier normalized phase normalized
no (hz) component component (deg) phase (deg)
1 6.000E+01 1.482E+01 1.000000 -0.005 0.000
2 1.200E+02 2.492E-03 0.000168 -104.347 -104.342
3 1.800E+02 6.465E-04 0.000044 -86.663 -86.658
4 2.400E+02 1.132E-03 0.000076 -61.324 -61.319
5 3.000E+02 1.185E-03 0.000080 -70.091 -70.086
6 3.600E+02 1.092E-03 0.000074 -63.607 -63.602
7 4.200E+02 1.220E-03 0.000082 -56.288 -56.283
8 4.800E+02 1.354E-03 0.000091 -54.669 -54.664
9 5.400E+02 1.467E-03 0.000099 -52.660 -52.655
Notice the extremely small harmonic and DC
components of this sinusoidal waveform. Ideally, there would
be nothing but the fundamental frequency showing (being a
perfect sine wave), but our Fourier analysis figures aren't
perfect because SPICE doesn't have the luxury of sampling a
waveform of infinite duration. Next, we'll compare this with
the Fourier analysis of the half-wave "rectified" voltage
across the load resistor:
fourier components of transient response v(2)
dc component = 4.456E+00
harmonic frequency fourier normalized phase normalized
no (hz) component component (deg) phase (deg)
1 6.000E+01 7.000E+00 1.000000 -0.195 0.000
2 1.200E+02 3.016E+00 0.430849 -89.765 -89.570
3 1.800E+02 1.206E-01 0.017223 -168.005 -167.810
4 2.400E+02 5.149E-01 0.073556 -87.295 -87.100
5 3.000E+02 6.382E-02 0.009117 -152.790 -152.595
6 3.600E+02 1.727E-01 0.024676 -79.362 -79.167
7 4.200E+02 4.492E-02 0.006417 -132.420 -132.224
8 4.800E+02 7.493E-02 0.010703 -61.479 -61.284
9 5.400E+02 4.051E-02 0.005787 -115.085 -114.889
Notice the relatively large even-multiple
harmonics in this analysis. By cutting out half of our AC
wave, we've introduced the equivalent of several
higher-frequency sinusoidal (actually, cosine) waveforms
into our circuit from the original, pure sine-wave. Also
take note of the large DC component: 4.456 volts. Because
our AC voltage waveform has been "rectified" (only allowed
to push in one direction across the load rather than
back-and-forth), it behaves a lot more like DC.
Another method of AC/DC conversion is called
full-wave, which as you may have guessed utilizes the
full cycle of AC power from the source, reversing the
polarity of half the AC cycle to get electrons to flow
through the load the same direction all the time. I won't
bore you with details of exactly how this is done, but we
can examine the waveform and its harmonic analysis through
SPICE:

fullwave bridge rectifier
v1 1 0 sin(0 15 60 0 0)
rload 2 3 10k
d1 1 2 mod1
d2 0 2 mod1
d3 3 1 mod1
d4 3 0 mod1
.model mod1 d
.tran .5m 17m
.plot tran v(1,0) v(2,3)
.four 60 v(2,3)
.end
legend:
*: v(1)
+: v(2,3)
time v(1)
(*)---------- -20 -10 0.000E+00 1.000E+01
(+)---------- 0.000E+00 5.000E+00 1.000E+01 1.500E+01
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 0.000E+00 + . * . .
5.000E-04 2.806E+00 . + . . * . .
1.000E-03 5.483E+00 . +. . * . .
1.500E-03 7.929E+00 . . + . * . .
2.000E-03 1.013E+01 . . + . * .
2.500E-03 1.198E+01 . . . + . * .
3.000E-03 1.338E+01 . . . + . * .
3.500E-03 1.435E+01 . . . + . *.
4.000E-03 1.476E+01 . . . + . *
4.500E-03 1.470E+01 . . . + . *.
5.000E-03 1.406E+01 . . . + . * .
5.500E-03 1.299E+01 . . . + . * .
6.000E-03 1.139E+01 . . + .* .
6.500E-03 9.455E+00 . . + . *. .
7.000E-03 7.113E+00 . . + . * . .
7.500E-03 4.591E+00 . + . . * . .
8.000E-03 1.841E+00 . + . . * . .
8.500E-03 -9.177E-01 . + . *. . .
9.000E-03 -3.689E+00 . + . * . . .
9.500E-03 -6.298E+00 . + * . . .
1.000E-02 -8.701E+00 . . * + . . .
1.050E-02 -1.079E+01 . *. +. . .
1.100E-02 -1.249E+01 . * . . + . .
1.150E-02 -1.377E+01 . * . . + . .
1.200E-02 -1.453E+01 . * . . + . .
1.250E-02 -1.482E+01 . * . . + . .
1.300E-02 -1.452E+01 . * . . + . .
1.350E-02 -1.378E+01 . * . . + . .
1.400E-02 -1.248E+01 . * . . + . .
1.450E-02 -1.081E+01 . *. +. . .
1.500E-02 -8.681E+00 . . * + . . .
1.550E-02 -6.321E+00 . + * . . .
1.600E-02 -3.666E+00 . + . * . . .
1.650E-02 -9.432E-01 . + . *. . .
1.700E-02 1.865E+00 . + . . * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
fourier components of transient response v(2,3)
dc component = 8.273E+00
harmonic frequency fourier normalized phase normalized
no (hz) component component (deg) phase (deg)
1 6.000E+01 7.000E-02 1.000000 -93.519 0.000
2 1.200E+02 5.997E+00 85.669415 -90.230 3.289
3 1.800E+02 7.241E-02 1.034465 -93.787 -0.267
4 2.400E+02 1.013E+00 14.465161 -92.492 1.027
5 3.000E+02 7.364E-02 1.052023 -95.026 -1.507
6 3.600E+02 3.337E-01 4.767350 -100.271 -6.752
7 4.200E+02 7.496E-02 1.070827 -94.023 -0.504
8 4.800E+02 1.404E-01 2.006043 -118.839 -25.319
9 5.400E+02 7.457E-02 1.065240 -90.907 2.612
What a difference! According to SPICE's
Fourier transform, we have a 2nd harmonic component to this
waveform that's over 85 times the amplitude of the original
AC source frequency! The DC component of this wave shows up
as being 8.273 volts (almost twice what is was for the
half-wave rectifier circuit) while the second harmonic is
almost 6 volts in amplitude. Notice all the other harmonics
further on down the table. The odd harmonics are actually
stronger at some of the higher frequencies than they are at
the lower frequencies, which is interesting.
As you can see, what may begin as a neat,
simple AC sine-wave may end up as a complex mess of
harmonics after passing through just a few electronic
components. While the complex mathematics behind all this
Fourier transformation is not necessary for the beginning
student of electric circuits to understand, it is of the
utmost importance to realize the principles at work and to
grasp the practical effects that harmonic signals may have
on circuits. The practical effects of harmonic frequencies
in circuits will be explored in the last section of this
chapter, but before we do that we'll take a closer look at
waveforms and their respective harmonics.
-
REVIEW:
-
Any waveform at all, so long as it
is repetitive, can be reduced to a series of sinusoidal
waveforms added together. Different waveshapes consist of
different blends of sine-wave harmonics.
-
Rectification of AC to DC is a very common
source of harmonics within industrial power systems.
|