Square wave signals
It has been found that any repeating,
non-sinusoidal waveform can be equated to a combination of
DC voltage, sine waves, and/or cosine waves (sine waves with
a 90 degree phase shift) at various amplitudes and
frequencies. This is true no matter how strange or
convoluted the waveform in question may be. So long as it
repeats itself regularly over time, it is reducible to this
series of sinusoidal waves. In particular, it has been found
that square waves are mathematically equivalent to the sum
of a sine wave at that same frequency, plus an infinite
series of odd-multiple frequency sine waves at diminishing
amplitude:

This truth about waveforms at first may seem
too strange to believe. However, if a square wave is
actually an infinite series of sine wave harmonics added
together, it stands to reason that we should be able to
prove this by adding together several sine wave harmonics to
produce a close approximation of a square wave. This
reasoning is not only sound, but easily demonstrated with
SPICE.
The circuit we'll be simulating is nothing
more than several sine wave AC voltage sources of the proper
amplitudes and frequencies connected together in series.
We'll use SPICE to plot the voltage waveforms across
successive additions of voltage sources, like this:
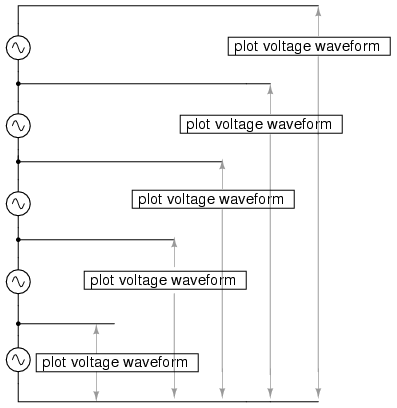
In this particular SPICE simulation, I've
summed the 1st, 3rd, 5th, 7th, and 9th harmonic voltage
sources in series for a total of five AC voltage sources.
The fundamental frequency is 50 Hz and each harmonic is, of
course, an integer multiple of that frequency. The amplitude
(voltage) figures are not random numbers; rather, they have
been arrived at through the equations shown in the frequency
series (the fraction 4/π multiplied by 1, 1/3, 1/5, 1/7,
etc. for each of the increasing odd harmonics).
building a squarewave
v1 1 0 sin (0 1.27324 50 0 0) 1st harmonic (50 Hz)
v3 2 1 sin (0 424.413m 150 0 0) 3rd harmonic
v5 3 2 sin (0 254.648m 250 0 0) 5th harmonic
v7 4 3 sin (0 181.891m 350 0 0) 7th harmonic
v9 5 4 sin (0 141.471m 450 0 0) 9th harmonic
r1 5 0 10k
.tran 1m 20m
.plot tran v(1,0) Plot 1st harmonic
.plot tran v(2,0) Plot 1st + 3rd harmonics
.plot tran v(3,0) Plot 1st + 3rd + 5th harmonics
.plot tran v(4,0) Plot 1st + 3rd + 5th + 7th harmonics
.plot tran v(5,0) Plot 1st + . . . + 9th harmonics
.end
I'll narrate the analysis step by step from
here, explaining what it is we're looking at. In this first
plot, we see the fundamental-frequency sine-wave of 50 Hz by
itself. It is nothing but a pure sine shape, with no
additional harmonic content. This is the kind of waveform
produced by an ideal AC power source:
time v(1) -1.000E+00 0.000E+00 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 0.000E+00 . . * . .
1.000E-03 3.915E-01 . . . * . .
2.000E-03 7.414E-01 . . . * . .
3.000E-03 1.020E+00 . . . * .
4.000E-03 1.199E+00 . . . . * .
5.000E-03 1.261E+00 . . . . * .
6.000E-03 1.199E+00 . . . . * .
7.000E-03 1.020E+00 . . . * .
8.000E-03 7.405E-01 . . . * . .
9.000E-03 3.890E-01 . . . * . .
1.000E-02 -5.819E-04 . . * . .
1.100E-02 -3.901E-01 . . * . . .
1.200E-02 -7.414E-01 . . * . . .
1.300E-02 -1.020E+00 . * . . .
1.400E-02 -1.199E+00 . * . . . .
1.500E-02 -1.261E+00 . * . . . .
1.600E-02 -1.199E+00 . * . . . .
1.700E-02 -1.020E+00 . * . . .
1.800E-02 -7.405E-01 . . * . . .
1.900E-02 -3.890E-01 . . * . . .
2.000E-02 5.819E-04 . . * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Next, we see what happens when this clean
and simple waveform is combined with the third harmonic
(three times 50 Hz, or 150 Hz). Suddenly, it doesn't look
like a clean sine wave any more:
time v(2) -1.000E+00 0.000E+00 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 0.000E+00 . . * . .
1.000E-03 7.199E-01 . . . * . .
2.000E-03 1.108E+00 . . . . * .
3.000E-03 1.135E+00 . . . . * .
4.000E-03 9.672E-01 . . . * .
5.000E-03 8.731E-01 . . . * . .
6.000E-03 9.751E-01 . . . * .
7.000E-03 1.144E+00 . . . . * .
8.000E-03 1.111E+00 . . . . * .
9.000E-03 6.995E-01 . . . * . .
1.000E-02 -5.697E-03 . . * . .
1.100E-02 -7.066E-01 . . * . . .
1.200E-02 -1.108E+00 . * . . . .
1.300E-02 -1.135E+00 . * . . . .
1.400E-02 -9.672E-01 . * . . .
1.500E-02 -8.731E-01 . . * . . .
1.600E-02 -9.751E-01 . * . . .
1.700E-02 -1.144E+00 . * . . . .
1.800E-02 -1.111E+00 . * . . . .
1.900E-02 -6.995E-01 . . * . . .
2.000E-02 5.697E-03 . . * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The rise and fall times between positive and
negative cycles are much steeper now, and the crests of the
wave are closer to becoming flat like a squarewave. Watch
what happens as we add the next odd harmonic frequency:
time v(3)
time v(3) -1.000E+00 0.000E+00 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 0.000E+00 . . * . .
1.000E-03 9.436E-01 . . . *. .
2.000E-03 1.095E+00 . . . .* .
3.000E-03 9.388E-01 . . . *. .
4.000E-03 9.807E-01 . . . * .
5.000E-03 1.069E+00 . . . .* .
6.000E-03 9.616E-01 . . . *. .
7.000E-03 9.479E-01 . . . *. .
8.000E-03 1.124E+00 . . . . * .
9.000E-03 8.957E-01 . . . *. .
1.000E-02 -1.925E-02 . . * . .
1.100E-02 -9.029E-01 . .* . . .
1.200E-02 -1.095E+00 . *. . . .
1.300E-02 -9.388E-01 . .* . . .
1.400E-02 -9.807E-01 . * . . .
1.500E-02 -1.069E+00 . *. . . .
1.600E-02 -9.616E-01 . .* . . .
1.700E-02 -9.479E-01 . .* . . .
1.800E-02 -1.124E+00 . * . . . .
1.900E-02 -8.957E-01 . .* . . .
2.000E-02 1.925E-02 . . * . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The most noticeable change here is how the
crests of the wave have flattened even more. There are more
several dips and crests at each end of the wave, but those
dips and crests are smaller in amplitude than they were
before. Watch again as we add the next odd harmonic waveform
to the mix:
time v(4) -1.000E+00 0.000E+00 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 0.000E+00 . . * . .
1.000E-03 1.055E+00 . . . .* .
2.000E-03 9.861E-01 . . . * .
3.000E-03 9.952E-01 . . . * .
4.000E-03 1.023E+00 . . . * .
5.000E-03 9.631E-01 . . . *. .
6.000E-03 1.044E+00 . . . .* .
7.000E-03 9.572E-01 . . . *. .
8.000E-03 1.031E+00 . . . * .
9.000E-03 9.962E-01 . . . * .
1.000E-02 -4.396E-02 . . *. . .
1.100E-02 -9.743E-01 . * . . .
1.200E-02 -9.861E-01 . * . . .
1.300E-02 -9.952E-01 . * . . .
1.400E-02 -1.023E+00 . * . . .
1.500E-02 -9.631E-01 . .* . . .
1.600E-02 -1.044E+00 . *. . . .
1.700E-02 -9.572E-01 . .* . . .
1.800E-02 -1.031E+00 . * . . .
1.900E-02 -9.962E-01 . * . . .
2.000E-02 4.396E-02 . . .* . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Here we can see the wave becoming flatter at
each peak. Finally, adding the 9th harmonic, the fifth sine
wave voltage source in our circuit, we obtain this result:
time v(5) -1.000E+00 0.000E+00 1.000E+00
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 0.000E+00 . . * . .
1.000E-03 1.079E+00 . . . .* .
2.000E-03 9.845E-01 . . . * .
3.000E-03 1.017E+00 . . . * .
4.000E-03 9.835E-01 . . . * .
5.000E-03 1.017E+00 . . . * .
6.000E-03 9.814E-01 . . . * .
7.000E-03 1.023E+00 . . . * .
8.000E-03 9.691E-01 . . . * .
9.000E-03 1.048E+00 . . . .* .
1.000E-02 -8.103E-02 . . *. . .
1.100E-02 -9.557E-01 . .* . . .
1.200E-02 -9.845E-01 . * . . .
1.300E-02 -1.017E+00 . * . . .
1.400E-02 -9.835E-01 . * . . .
1.500E-02 -1.017E+00 . * . . .
1.600E-02 -9.814E-01 . * . . .
1.700E-02 -1.023E+00 . * . . .
1.800E-02 -9.691E-01 . * . . .
1.900E-02 -1.048E+00 . *. . . .
2.000E-02 8.103E-02 . . .* . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The end result of adding the first five odd
harmonic waveforms together (all at the proper amplitudes,
of course) is a close approximation of a square wave. The
point in doing this is to illustrate how we can build a
square wave up from multiple sine waves at different
frequencies, to prove that a pure square wave is actually
equivalent to a series of sine waves. When a square
wave AC voltage is applied to a circuit with reactive
components (capacitors and inductors), those components
react as if they were being exposed to several sine wave
voltages of different frequencies, which in fact they are.
The fact that repeating, non-sinusoidal
waves are equivalent to a definite series of additive DC
voltage, sine waves, and/or cosine waves is a consequence of
how waves work: a fundamental property of all wave-related
phenomena, electrical or otherwise. The mathematical process
of reducing a non-sinusoidal wave into these constituent
frequencies is called Fourier analysis, the details
of which are well beyond the scope of this text. However,
computer algorithms have been created to perform this
analysis at high speeds on real waveforms, and its
application in AC power quality and signal analysis is
widespread.
SPICE has the ability to sample a waveform
and reduce it into its constituent sine wave harmonics by
way of a Fourier Transform algorithm, outputting the
frequency analysis as a table of numbers. Let's try this on
a square wave, which we already know is composed of
odd-harmonic sine waves:
squarewave analysis netlist
v1 1 0 pulse (-1 1 0 .1m .1m 10m 20m)
r1 1 0 10k
.tran 1m 40m
.plot tran v(1,0)
.four 50 v(1,0)
.end
he pulse option in the netlist line
describing voltage source v1 instructs SPICE to
simulate a square-shaped "pulse" waveform, in this case one
that is symmetrical (equal time for each half-cycle) and has
a peak amplitude of 1 volt. First we'll plot the square wave
to be analyzed:
time v(1) -1 -0.5 0 0.5 1
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0.000E+00 -1.000E+00 * . . . .
1.000E-03 1.000E+00 . . . . *
2.000E-03 1.000E+00 . . . . *
3.000E-03 1.000E+00 . . . . *
4.000E-03 1.000E+00 . . . . *
5.000E-03 1.000E+00 . . . . *
6.000E-03 1.000E+00 . . . . *
7.000E-03 1.000E+00 . . . . *
8.000E-03 1.000E+00 . . . . *
9.000E-03 1.000E+00 . . . . *
1.000E-02 1.000E+00 . . . . *
1.100E-02 -1.000E+00 * . . . .
1.200E-02 -1.000E+00 * . . . .
1.300E-02 -1.000E+00 * . . . .
1.400E-02 -1.000E+00 * . . . .
1.500E-02 -1.000E+00 * . . . .
1.600E-02 -1.000E+00 * . . . .
1.700E-02 -1.000E+00 * . . . .
1.800E-02 -1.000E+00 * . . . .
1.900E-02 -1.000E+00 * . . . .
2.000E-02 -1.000E+00 * . . . .
2.100E-02 1.000E+00 . . . . *
2.200E-02 1.000E+00 . . . . *
2.300E-02 1.000E+00 . . . . *
2.400E-02 1.000E+00 . . . . *
2.500E-02 1.000E+00 . . . . *
2.600E-02 1.000E+00 . . . . *
2.700E-02 1.000E+00 . . . . *
2.800E-02 1.000E+00 . . . . *
2.900E-02 1.000E+00 . . . . *
3.000E-02 1.000E+00 . . . . *
3.100E-02 -1.000E+00 * . . . .
3.200E-02 -1.000E+00 * . . . .
3.300E-02 -1.000E+00 * . . . .
3.400E-02 -1.000E+00 * . . . .
3.500E-02 -1.000E+00 * . . . .
3.600E-02 -1.000E+00 * . . . .
3.700E-02 -1.000E+00 * . . . .
3.800E-02 -1.000E+00 * . . . .
3.900E-02 -1.000E+00 * . . . .
4.000E-02 -1.000E+00 * . . . .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Next, we'll print the Fourier analysis
generated by SPICE for this square wave:
fourier components of transient response v(1)
dc component = -2.439E-02
harmonic frequency fourier normalized phase normalized
no (hz) component component (deg) phase (deg)
1 5.000E+01 1.274E+00 1.000000 -2.195 0.000
2 1.000E+02 4.892E-02 0.038415 -94.390 -92.195
3 1.500E+02 4.253E-01 0.333987 -6.585 -4.390
4 2.000E+02 4.936E-02 0.038757 -98.780 -96.585
5 2.500E+02 2.562E-01 0.201179 -10.976 -8.780
6 3.000E+02 5.010E-02 0.039337 -103.171 -100.976
7 3.500E+02 1.841E-01 0.144549 -15.366 -13.171
8 4.000E+02 5.116E-02 0.040175 -107.561 -105.366
9 4.500E+02 1.443E-01 0.113316 -19.756 -17.561
total harmonic distortion = 43.805747 percent
Here, SPICE has broken the waveform down
into a spectrum of sinusoidal frequencies up to the ninth
harmonic, plus a small DC voltage labelled DC component.
I had to inform SPICE of the fundamental frequency (for a
square wave with a 20 millisecond period, this frequency is
50 Hz), so it knew how to classify the harmonics. Note how
small the figures are for all the even harmonics (2nd, 4th,
6th, 8th), and how the amplitudes of the odd harmonics
diminish (1st is largest, 9th is smallest).
This same technique of "Fourier
Transformation" is often used in computerized power
instrumentation, sampling the AC waveform(s) and determining
the harmonic content thereof. A common computer algorithm
(sequence of program steps to perform a task) for this is
the Fast Fourier Transform or FFT function.
You need not be concerned with exactly how these computer
routines work, but be aware of their existence and
application.
This same mathematical technique used in
SPICE to analyze the harmonic content of waves can be
applied to the technical analysis of music: breaking up any
particular sound into its constituent sine-wave frequencies.
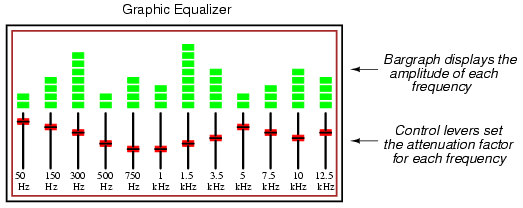
In fact, you may have already seen a device designed to do
just that without realizing what it was! A graphic
equalizer is a piece of high-fidelity stereo equipment
that controls (and sometimes displays) the nature of music's
harmonic content. Equipped with several knobs or slide
levers, the equalizer is able to selectively attenuate
(reduce) the amplitude of certain frequencies present in
music, to "customize" the sound for the listener's benefit.
Typically, there will be a "bar graph" display next to each
control lever, displaying the amplitude of each particular
frequency.
A device built strictly to display -- not
control -- the amplitudes of each frequency range for a
mixed-frequency signal is typically called a spectrum
analyzer. The design of spectrum analyzers may be as
simple as a set of "filter" circuits (see the next chapter
for details) designed to separate the different frequencies
from each other, or as complex as a special-purpose digital
computer running an FFT algorithm to mathematically split
the signal into its harmonic components. Spectrum analyzers
are often designed to analyze extremely high-frequency
signals, such as those produced by radio transmitters and
computer network hardware. In that form, they often have an
appearance like that of an oscilloscope:
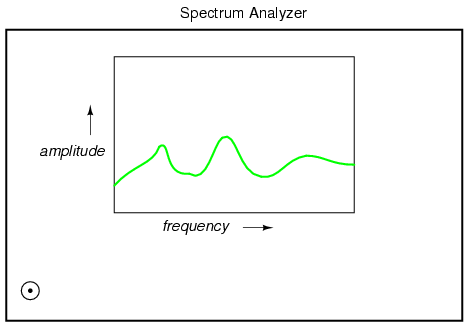
Like an oscilloscope, the spectrum analyzer
uses a CRT (or a computer display mimicking a CRT) to
display a plot of the signal. Unlike an oscilloscope, this
plot is amplitude over frequency rather than
amplitude over time. In essence, a frequency analyzer
gives the operator a Bode plot of the signal: something an
engineer might call a frequency-domain rather than a
time-domain analysis.
The term "domain" is mathematical: a
sophisticated word to describe the horizontal axis of a
graph. Thus, an oscilloscope's plot of amplitude (vertical)
over time (horizontal) is a "time-domain" analysis, whereas
a spectrum analyzer's plot of amplitude (vertical) over
frequency (horizontal) is a "frequency-domain" analysis.
When we use SPICE to plot signal amplitude (either voltage
or current amplitude) over a range of frequencies, we are
performing frequency-domain analysis.
Please take note of how the Fourier analysis
from the last SPICE simulation isn't "perfect." Ideally, the
amplitudes of all the even harmonics should be absolutely
zero, and so should the DC component. Again, this is not so
much a quirk of SPICE as it is a property of waveforms in
general. A waveform of infinite duration (infinite number of
cycles) can be analyzed with absolute precision, but the
less cycles available to the computer for analysis, the less
precise the analysis. It is only when we have an equation
describing a waveform in its entirety that Fourier analysis
can reduce it to a definite series of sinusoidal waveforms.
The fewer times that a wave cycles, the less certain its
frequency is. Taking this concept to its logical extreme, a
short pulse -- a waveform that doesn't even complete a cycle
-- actually has no frequency, but rather acts as an
infinite range of frequencies. This principle is common to
all wave-based phenomena, not just AC voltages and
currents.
Suffice it to say that the number of cycles
and the certainty of a waveform's frequency component(s) are
directly related. We could improve the precision of our
analysis here by letting the wave oscillate on and on for
many cycles, and the result would be a spectrum analysis
more consistent with the ideal. In the following analysis,
I've omitted the waveform plot for brevity's sake -- it's
just a really long square wave:
squarewave
v1 1 0 pulse (-1 1 0 .1m .1m 10m 20m)
r1 1 0 10k
.option limpts=1001
.tran 1m 1
.plot tran v(1,0)
.four 50 v(1,0)
.end
fourier components of transient response v(1)
dc component = 9.999E-03
harmonic frequency fourier normalized phase normalized
no (hz) component component (deg) phase (deg)
1 5.000E+01 1.273E+00 1.000000 -1.800 0.000
2 1.000E+02 1.999E-02 0.015704 86.382 88.182
3 1.500E+02 4.238E-01 0.332897 -5.400 -3.600
4 2.000E+02 1.997E-02 0.015688 82.764 84.564
5 2.500E+02 2.536E-01 0.199215 -9.000 -7.200
6 3.000E+02 1.994E-02 0.015663 79.146 80.946
7 3.500E+02 1.804E-01 0.141737 -12.600 -10.800
8 4.000E+02 1.989E-02 0.015627 75.529 77.329
9 4.500E+02 1.396E-01 0.109662 -16.199 -14.399
Notice how this analysis shows less of a DC
component voltage and lower amplitudes for each of the even
harmonic frequency sine waves, all because we let the
computer sample more cycles of the wave. Again, the
imprecision of the first analysis is not so much a flaw in
SPICE as it is a fundamental property of waves and of signal
analysis.
-
REVIEW:
-
Square waves are equivalent to a sine wave
at the same (fundamental) frequency added to an infinite
series of odd-multiple sine-wave harmonics at decreasing
amplitudes.
-
Computer algorithms exist which are able
to sample waveshapes and determine their constituent
sinusoidal components. The Fourier Transform
algorithm (particularly the Fast Fourier Transform,
or FFT) is commonly used in computer circuit
simulation programs such as SPICE and in electronic
metering equipment for determining power quality.
|