Phase shift

PARTS AND MATERIALS

• Low-voltage AC power supply

• Two capacitors, 0.1 �F each, non-polarized (Radio Shack catalog # 272-135)

• Two 27 kΩ resistors

I recommend ceramic disk capacitors, because they are insensitive to polarity (non-polarized), inexpensive, and durable. Avoid capacitors with any kind of polarity marking, as these will be destroyed when powered by AC!

CROSS-REFERENCES

Lessons In Electric Circuits, Volume 2, chapter 1: "Basic AC Theory"

Lessons In Electric Circuits, Volume 2, chapter 4: "Reactance and Impedance -- Capacitive"

LEARNING OBJECTIVES

• How out-of-phase AC voltages do not add algebraically, but according to vector (phasor) arithmetic

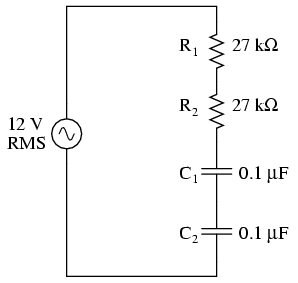
SCHEMATIC DIAGRAM

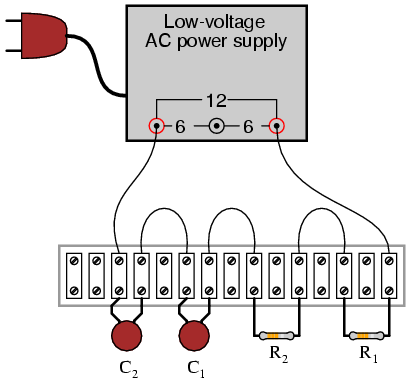
ILLUSTRATION

INSTRUCTIONS

Build the circuit and measure voltage drops across each component with an AC voltmeter. Measure total (supply) voltage with the same voltmeter. You will discover that the voltage drops do not add up to equal the total voltage. This is due to phase shifts in the circuit: voltage dropped across the capacitors is out-of-phase with voltage dropped across the resistors, and thus the voltage drop figures do not add up as one might expect. Taking phase angle into consideration, they do add up to equal the total, but a voltmeter doesn't provide phase angle measurements, only amplitude.

Try measuring voltage dropped across both resistors at once. This voltage drop will equal the sum of the voltage drops measured across each resistor separately. This tells you that both the resistors' voltage drop waveforms are in-phase with each other, since they add simply and directly.

Measure voltage dropped across both capacitors at once. This voltage drop, like the drop measured across the two resistors, will equal the sum of the voltage drops measured across each capacitor separately. Likewise, this tells you that both the capacitors' voltage drop waveforms are in-phase with each other.

Given that the power supply frequency is 60 Hz (household power frequency in the United States), calculate impedances for all components and determine all voltage drops using Ohm's Law (E=IZ ; I=E/Z ; Z=E/I). The polar magnitudes of the results should closely agree with your voltmeter readings.

COMPUTER SIMULATION

Schematic with SPICE node numbers:

The two large-value resistors R_bogus1 and R_bogus1 are connected across the capacitors to provide a DC path to ground in order that SPICE will work. This is a "fix" for one of SPICE's quirks, to avoid it from seeing the capacitors as open circuits in its analysis. These two resistors are entirely unnecessary in the real circuit.

Netlist (make a text file containing the following text, verbatim):

phase shift
v1 1 0 ac 12 sin
r1 1 2 27k
r2 2 3 27k
c1 3 4 0.1u
c2 4 0 0.1u
rbogus1 3 4 1e9
rbogus2 4 0 1e9
.ac lin 1 60 60
* Voltage across each component:
.print ac v(1,2) v(2,3) v(3,4) v(4,0) 
* Voltage across pairs of similar components
.print ac v(1,3) v(3,0)  
.end