TTL NOR and OR gates

Let's examine the following TTL circuit and analyze its operation:

Transistors Q₁ and Q₂ are both arranged in the same manner that we've seen for transistor Q₁ in all the other TTL circuits. Rather than functioning as amplifiers, Q₁ and Q₂ are both being used as two-diode "steering" networks. We may replace Q₁ and Q₂ with diode sets to help illustrate:

If input A is left floating (or connected to V_cc), current will go through the base of transistor Q₃, saturating it. If input A is grounded, that current is diverted away from Q₃'s base through the left steering diode of "Q₁," thus forcing Q₃ into cutoff. The same can be said for input B and transistor Q₄: the logic level of input B determines Q₄'s conduction: either saturated or cutoff.

Notice how transistors Q₃ and Q₄ are paralleled at their collector and emitter terminals. In essence, these two transistors are acting as paralleled switches, allowing current through resistors R₃ and R₄ according to the logic levels of inputs A and B. If any input is at a "high" (1) level, then at least one of the two transistors (Q₃ and/or Q₄) will be saturated, allowing current through resistors R₃ and R₄, and turning on the final output transistor Q₅ for a "low" (0) logic level output. The only way the output of this circuit can ever assume a "high" (1) state is if both Q₃ and Q₄ are cutoff, which means both inputs would have to be grounded, or "low" (0).

This circuit's truth table, then, is equivalent to that of the NOR gate:

In order to turn this NOR gate circuit into an OR gate, we would have to invert the output logic level with another transistor stage, just like we did with the NAND-to-AND gate example:

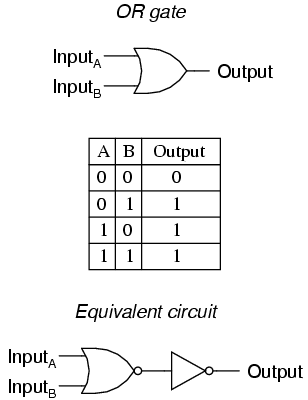
The truth table and equivalent gate circuit (an inverted-output NOR gate) are shown here:

Of course, totem-pole output stages are also possible in both NOR and OR TTL logic circuits.

• REVIEW:

• An OR gate may be created by adding an inverter stage to the output of the NOR gate circuit.