A third variation on the counter-DAC-based
converter theme is, in my estimation, the most elegant. Instead of a regular
"up" counter driving the DAC, this circuit uses an up/down counter. The
counter is continuously clocked, and the up/down control line is driven by
the output of the comparator. So, when the analog input signal exceeds the
DAC output, the counter goes into the "count up" mode. When the DAC output
exceeds the analog input, the counter switches into the "count down" mode.
Either way, the DAC output always counts in the proper direction to track
the input signal.
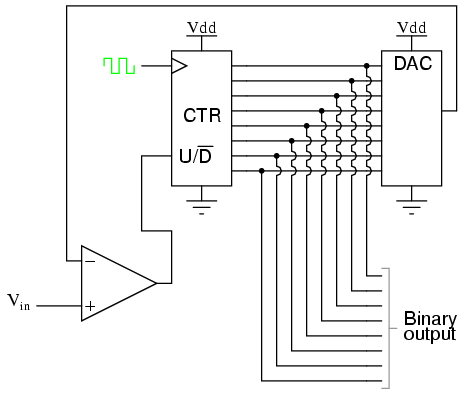
Notice how no shift register is needed to buffer the binary count at the
end of a cycle. Since the counter's output continuously tracks the input
(rather than counting to meet the input and then resetting back to zero),
the binary output is legitimately updated with every clock pulse.
An advantage of this converter circuit is speed, since the counter never
has to reset. Note the behavior of this circuit:
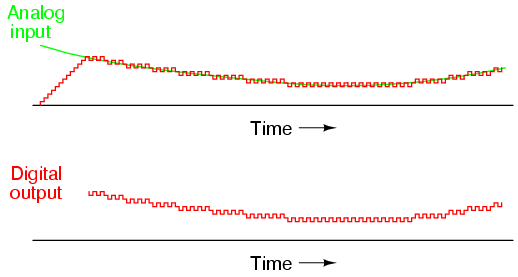
Note the much faster update time than any of the other "counting" ADC
circuits. Also note how at the very beginning of the plot where the counter
had to "catch up" with the analog signal, the rate of change for the output
was identical to that of the first counting ADC. Also, with no shift
register in this circuit, the binary output would actually ramp up rather
than jump from zero to an accurate count as it did with the counter and
successive approximation ADC circuits.
Perhaps the greatest drawback to this ADC design is the fact that the
binary output is never stable: it always switches between counts with every
clock pulse, even with a perfectly stable analog input signal. This
phenomenon is informally known as bit bobble, and it can be
problematic in some digital systems.
This tendency can be overcome, though, through the creative use of a
shift register. For example, the counter's output may be latched through a
parallel-in/parallel-out shift register only when the output changes by two
or more steps. Building a circuit to detect two or more successive counts in
the same direction takes a little ingenuity, but is worth the effort. |