Voltage divider
PARTS AND MATERIALS
I'm purposely restricting the resistance
values between 1 kΩ and 100 kΩ for the sake of obtaining
accurate voltage and current readings with your meter. With
very low resistance values, the internal resistance of the
ammeter has a significant impact on measurement accuracy.
Very high resistance values may cause problems for voltage
measurement, the internal resistance of the voltmeter
substantially changing circuit resistance when it is
connected in parallel with a high-value resistor.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume
1, chapter 6: "Divider Circuits and Kirchhoff's Laws"
LEARNING OBJECTIVES
SCHEMATIC DIAGRAM
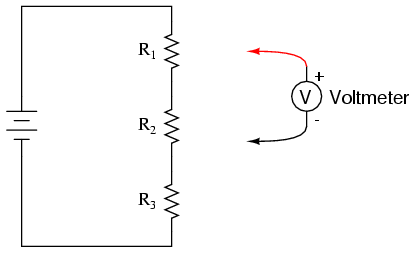
ILLUSTRATION
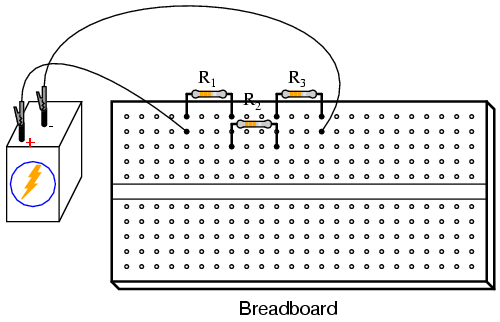

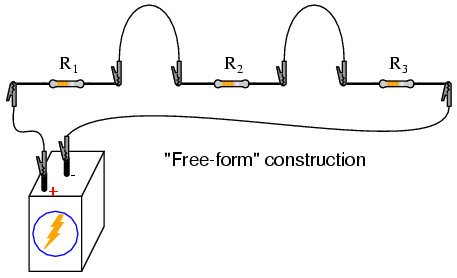
INSTRUCTIONS
Shown here are three different methods of
circuit construction: on a breadboard, on a terminal strip,
and "free-form." Try building the same circuit each way to
familiarize yourself with the different construction
techniques and their respective merits. The "free-form"
method -- where all components are connected together with
"alligator-" style jumper wires -- is the least
professional, but appropriate for a simple experiment such
as this. Breadboard construction is versatile and allows for
high component density (many parts in a small space), but is
quite temporary. Terminal strips offer a much more permanent
form of construction at the cost of low component density.
Select three resistors from your resistor
assortment and measure the resistance of each one with an
ohmmeter. Note these resistance values with pen and paper,
for reference in your circuit calculations.
Connect the three resistors in series, and
to the 6-volt battery, as shown in the illustrations.
Measure battery voltage with a voltmeter after the resistors
have been connected to it, noting this voltage figure on
paper as well. It is advisable to measure battery voltage
while it's powering the resistor circuit because this
voltage may differ slightly from a no-load condition. We saw
this effect exaggerated in the "parallel battery" experiment
while powering a high-wattage lamp: battery voltage tends to
"sag" or "droop" under load. Although this three-resistor
circuit should not present a heavy enough load (not enough
current drawn) to cause significant voltage "sag," measuring
battery voltage under load is a good scientific practice
because it provides more realistic data.
Use Ohm's Law (I=E/R) to calculate circuit
current, then verify this calculated value by measuring
current with an ammeter like this ("terminal strip" version
of the circuit shown as an arbitrary choice in construction
method):

If your resistor values are indeed between 1
kΩ and 100 kΩ, and the battery voltage approximately 6
volts, the current should be a very small value, in the
milliamp (mA) or microamp (�A) range. When you measure
current with a digital meter, the meter may show the
appropriate metric prefix symbol (m or �) in some corner of
the display. These metric prefix telltales are easy to
overlook when reading the display of a digital meter, so pay
close attention!
The measured value of current should agree
closely with your Ohm's Law calculation. Now, take that
calculated value for current and multiply it by the
respective resistances of each resistor to predict their
voltage drops (E=IR). Switch you multimeter to the "voltage"
mode and measure the voltage dropped across each resistor,
verifying the accuracy of your predictions. Again, there
should be close agreement between the calculated and
measured voltage figures.
Each resistor voltage drop will be some
fraction or percentage of the total voltage, hence the name
voltage divider given to this circuit. This
fractional value is determined by the resistance of the
particular resistor and the total resistance. If a resistor
drops 50% of the total battery voltage in a voltage divider
circuit, that proportion of 50% will remain the same as long
as the resistor values are not altered. So, if the total
voltage is 6 volts, the voltage across that resistor will be
50% of 6, or 3 volts. If the total voltage is 20 volts, that
resistor will drop 10 volts, or 50% of 20 volts.
The next part of this experiment is a
validation of Kirchhoff's Voltage Law. For this, you need to
identify each unique point in the circuit with a number.
Points that are electrically common (directly connected to
each other with insignificant resistance between) must bear
the same number. An example using the numbers 0 through 3 is
shown here in both illustrative and schematic form. In the
illustration, I show how points in the circuit may be
labeled with small pieces of tape, numbers written on the
tape:
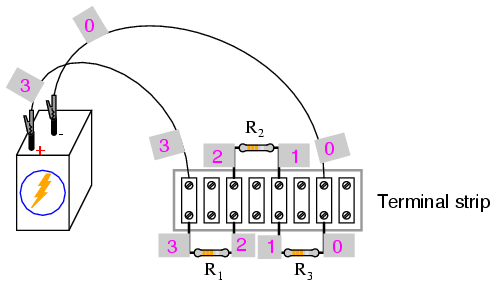

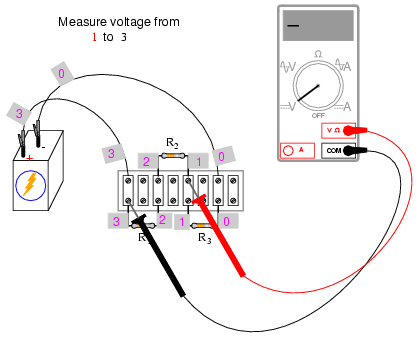
Using a digital voltmeter (this is
important!), measure voltage drops around the loop formed by
the points 0-1-2-3-0. Write on paper each of these voltages,
along with its respective sign as indicated by the meter. In
other words, if the voltmeter registers a negative voltage
such as -1.325 volts, you should write that figure as a
negative number. Do not reverse the meter probe
connections with the circuit to make the number read
"correctly." Mathematical sign is very significant in this
phase of the experiment! Here is a sequence of illustrations
showing how to "step around" the circuit loop, starting and
ending at point 0:
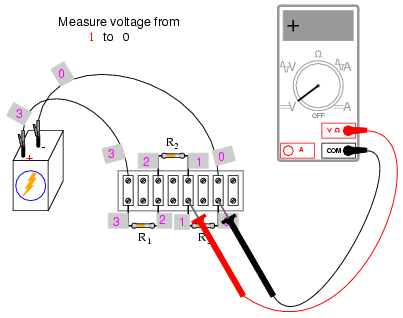
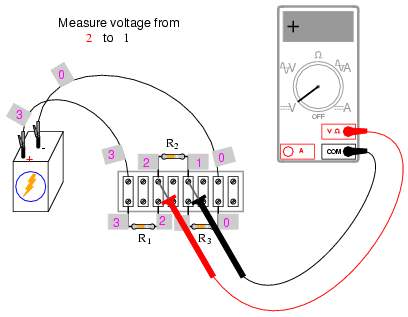
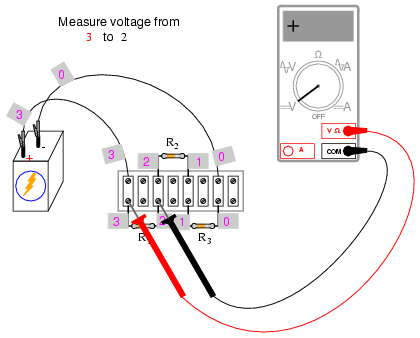
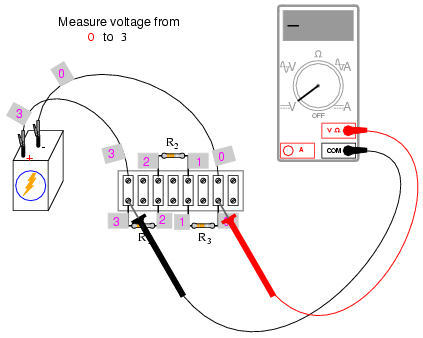
Using the voltmeter to "step" around the
circuit in this manner yields three positive voltage figures
and one negative:
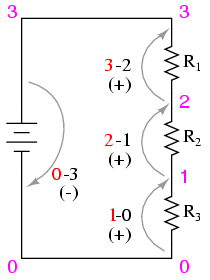
These figures, algebraically added
("algebraically" = respecting the signs of the numbers),
should equal zero. This is the fundamental principle of
Kirchhoff's Voltage Law: that the algebraic sum of all
voltage drops in a "loop" add to zero.
It is important to realize that the "loop"
stepped around does not have to be the same path that
current takes in the circuit, or even a legitimate current
path at all. The loop in which we tally voltage drops can be
any collection of points, so long as it begins and
ends with the same point. For example, we may measure and
add the voltages in the loop 1-2-3-1, and they will form a
sum of zero as well:
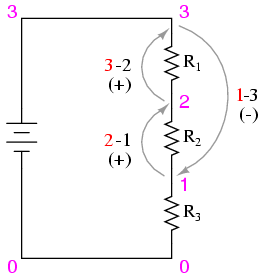


Try stepping between any set of points, in
any order, around your circuit and see for yourself that the
algebraic sum always equals zero. This Law holds true no
matter what the configuration of the circuit: series,
parallel, series-parallel, or even an irreducible network.
Kirchhoff's Voltage Law is a powerful
concept, allowing us to predict the magnitude and polarity
of voltages in a circuit by developing mathematical
equations for analysis based on the truth of all voltages in
a loop adding up to zero. This experiment is intended to
give empirical evidence for and a deep understanding of
Kirchhoff's Voltage Law as a general principle.
COMPUTER SIMULATION
Netlist (make a text file containing the
following text, verbatim):
Voltage divider
v1 3 0
r1 3 2 5k
r2 2 1 3k
r3 1 0 2k
.dc v1 6 6 1
* Voltages around 0-1-2-3-0 loop algebraically add to zero:
.print dc v(1,0) v(2,1) v(3,2) v(0,3)
* Voltages around 1-2-3-1 loop algebraically add to zero:
.print dc v(2,1) v(3,2) v(1,3)
.end
This computer simulation is based on the
point numbers shown in the previous diagrams for
illustrating Kirchhoff's Voltage Law (points 0 through 3).
Resistor values were chosen to provide 50%, 30%, and 20%
proportions of total voltage across R1, R2,
and R3, respectively. Feel free to modify the
voltage source value (in the ".dc" line, shown here
as 6 volts), and/or the resistor values.
When run, SPICE will print a line of text
containing four voltage figures, then another line of text
containing three voltage figures, along with lots of other
text lines describing the analysis process. Add the voltage
figures in each line to see that the sum is zero. |