A very simple computer
PARTS AND MATERIALS
-
Three batteries, each one with a different
voltage
-
Three equal-value resistors, between 10 kΩ
and 47 kΩ each
When selecting resistors, measure each one
with an ohmmeter and choose three that are the closest in
value to each other. Precision is very important for this
experiment!
CROSS-REFERENCES
Lessons In Electric Circuits, Volume
1, chapter 10: "DC Network Analysis"
LEARNING OBJECTIVES
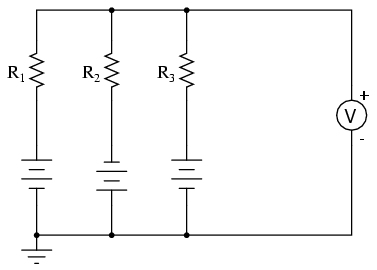
SCHEMATIC DIAGRAM
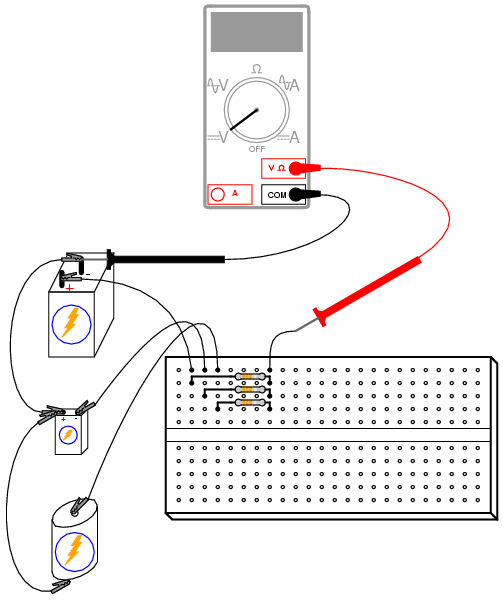
ILLUSTRATION
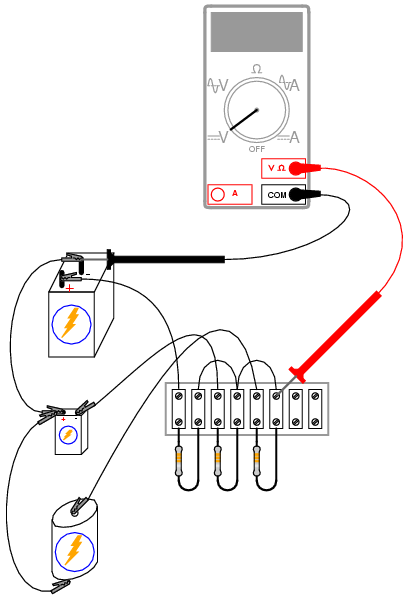
INSTRUCTIONS
This deceptively crude circuit performs the
function of mathematically averaging three voltage
signals together, and so fulfills a specialized
computational role. In other words, it is a computer that
can only do one mathematical operation: averaging three
quantities together.
Build this circuit as shown and measure all
battery voltages with a voltmeter. Write these voltage
figures on paper and average them together (E1 +
E2 + E3, divided by three). When you
measure each battery voltage, keep the black test probe
connected to the "ground" point (the side of the battery
directly joined to the other batteries by jumper wires), and
touch the red probe to the other battery terminal. Polarity
is important here! You will notice one battery in the
schematic diagram connected "backward" to the other two,
negative side "up." This battery's voltage should read as a
negative quantity when measured by a properly connected
digital meter, the other batteries measuring positive.
When the voltmeter is connected to the
circuit at the point shown in the schematic and
illustrations, it should register the algebraic average of
the three batteries' voltages. If the resistor values are
chosen to match each other very closely, the "output"
voltage of this circuit should match the calculated average
very closely as well.
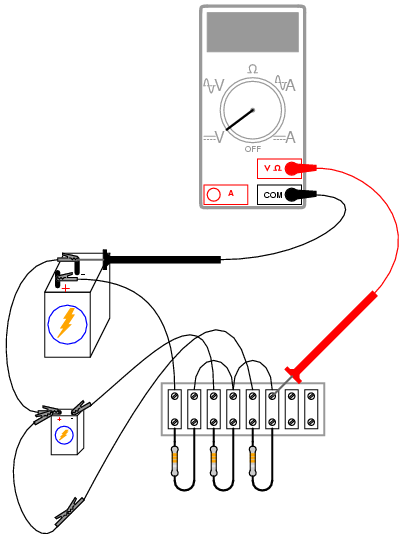
If one battery is disconnected, the output
voltage will equal the average voltage of the remaining
batteries. If the jumper wires formerly connecting the
removed battery to the averager circuit are connected to
each other, the circuit will average the two remaining
voltages together with 0 volts, producing a smaller output
signal:
The sheer simplicity of this circuit deters
most people from calling it a "computer," but it undeniably
performs the mathematical function of averaging. Not only
does it perform this function, but it performs it much
faster than any modern digital computer can! Digital
computers, such as personal computers (PCs) and pushbutton
calculators, perform mathematical operations in a series of
discrete steps. Analog computers perform calculations in
continuous fashion, exploiting Ohm's and Kirchhoff's Laws
for an arithmetic purpose, the "answer" computed as fast as
voltage propagates through the circuit (ideally, at the
speed of light!).
With the addition of circuits called
amplifiers, voltage signals in analog computer networks
may be boosted and re-used in other networks to perform a
wide variety of mathematical functions. Such analog
computers excel at performing the calculus operations of
numerical differentiation and integration, and as such may
be used to simulate the behavior of complex mechanical,
electrical, and even chemical systems. At one time, analog
computers were the ultimate tool for engineering research,
but since then have been largely supplanted by digital
computer technology. Digital computers enjoy the advantage
of performing mathematical operations with much better
precision than analog computers, albeit at much slower
theoretical speeds.
COMPUTER SIMULATION
Schematic with SPICE node numbers:
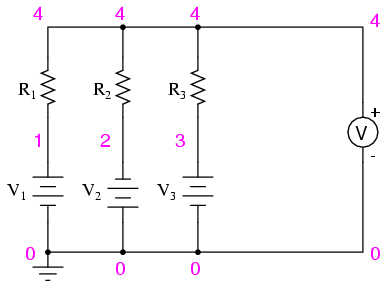
Netlist (make a text file containing the
following text, verbatim):
Voltage averager
v1 1 0
v2 0 2 dc 9
v3 3 0 dc 1.5
r1 1 4 10k
r2 2 4 10k
r3 3 4 10k
.dc v1 6 6 1
.print dc v(4,0)
.end
With this SPICE netlist, we can force a
digital computer to simulate and analog computer, which
averages three numbers together. Obviously, we aren't doing
this for the practical task of averaging numbers, but rather
to learn more about circuits and more about computer
simulation of circuits!
|